電気入門
総合情報.com

電気の基礎入門及び電気工事士資格対策サイトです。

令和7年度下期

問題1

図のような回路で，端子 間の合成抵抗a - b［Ω］は。



• イ.1
• ロ.2
• ハ.3
• ニ.4

---

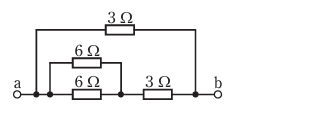
【解説】

合成抵抗を求める問題です。
合成抵抗を求める問題の基本は内側の抵抗から順に外側の抵抗を求めていきます。

のように
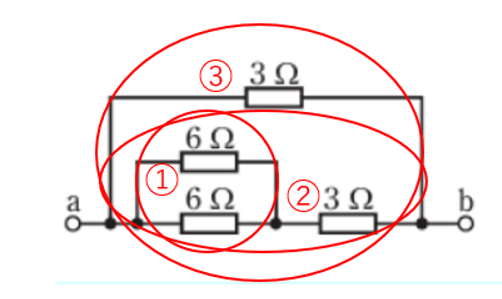
①→②→③
の順に求めていきます。
①6Ωと6Ωの並列接続です。
6 x 6 / 6 + 6 = 36 / 12 = 3Ω 次に②では
①で求めた3Ωと3Ωの直列接続です。
②3Ω+3Ω=6Ω
次に③では②で求めた6Ωと3Ωの並列接続です。
6 x 3 / 6 + 3 = 18 / 9 = 2Ω
になり答えはロの2です。

【答え・ロ】

問題2

抵抗R［Ω]に電圧V［V］を加えると，電流I［A］が流れ，P［W］の電力が消費される場合，抵抗R［Ω］を示す式として，誤っているものは。
• イ.PI/V
• ロ.P/I²
• ハ.V²/P
• ニ.V/I

---

【解説】

まず電力の公式とオームの法則を知っておかないといけません。

つまり、この問題はこれらの公式を代入して抵抗R[Ω]を導かないといけません。
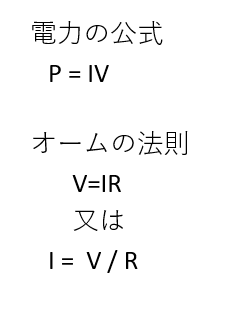
V=IR
順番に見ていくと

P = IV
P = I x IR
P = I²R
になり
R = P / I²・・・・・(ロ)

P = IV
P = (V / R) x V
P = V²/ R
PR = V²
R = V² / P・・・・・(ハ)

V = IR
R = V / I・・・・・・・・・・・(二)
となり(イ)のみ導くことができません。
したがって誤っているのは(イ)です。

【答え・イ】

問題3

電熱器により，60 kgの水の温度を20 K上昇させるのに必要な電力量［kW･h］は。
ただし，水の比熱は 4.2 kJ /(kg・K)とし，熱効率は100 ％とする。
• イ.1.0
• ロ.1.2
• ハ.1.4
• ニ.1.6

---

【解説】

まずポイントは
1㎏の水は、1リットル
です。
したがって
60kgの水は60リットル
になります。
今回は熱効率100%とあるので
100%の能力ということになります。
問題文で20K上昇させるための必要な電力量を求めます。
あと水の比熱は 4.2 kJ /(kg・K)と記載があるので
60 x 20 x 4.2=5040kJ
でここでさらにポイントがあります。
これは1秒間の電力量です。
問題では
［kW･h］
とありhは1時間です。
したがって1時間に直さないといけないので
60秒(1分) x 60分=3600秒(1時間)
になるので
5040 / 3600=1.4［kW･h］
になります。

【答え・ハ】

問題4

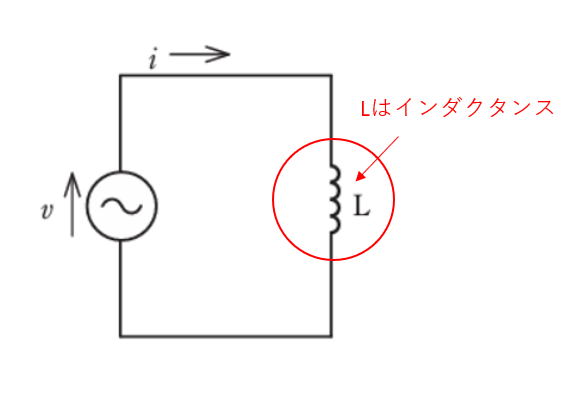
図のような正弦波交流回路の電源電圧 v に対する電流iの波形として，正しいものは。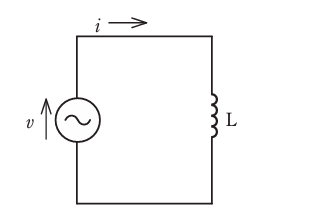

---

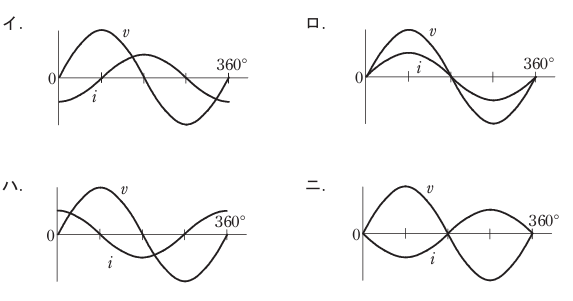
【解説】

回路にLインダクタンスが接続されています。

これは、電流iの波形は電源電圧vより、９０°位相が遅れます。
つまりvの波形よりiの波形が遅れているやつを探せばいいことになりますので

したがってイが正しいです。

【答え・イ】

問題5

図のような三相負荷に三相交流電圧を加えたとき，各線に20 Aの電流が流れた。線間電圧E［V］は。



• イ.120
• ロ.173
• ハ.208
• ニ.240

---

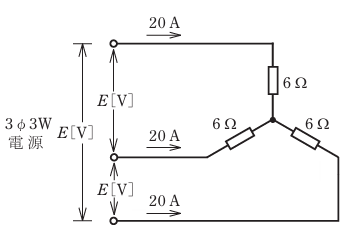
【解説】

問題はスター結線(Y結線)で線電流を求める問題です。
スター結線の場合は以下のことは必ず覚えておかなければなりません。
線電流=相電流
線間電圧=√3相電圧

つまりまず相電圧を求めて√3倍すれば線間電圧を求めることができます。
まず回路図より
線電流が20Aなので相電流も20A
です。
つぎに
今回は抵抗が6Ωなので
相電圧は
V=IR
より
V=20 x 6 = 120V(相電圧)
それの√3倍が線間電圧になるので
線間電圧=√3 x 120=207.8[V]
は約208[V]になります。

【答え・ハ】

問題6

図のような三相3線式回路について，図中のx印の箇所で断線した場合，負荷の全消費電力［kW］は。
ただし，負荷の抵抗は，30Ω とし，配線の抵抗は無視し，電源電圧は一定とする。



• イ.0.7
• ロ.0.9
• ハ.1.3
• ニ.2.0

---

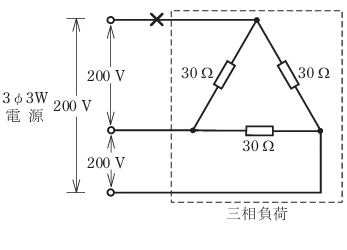
【解説】

三相3線式回路のうち、１つが断線すると、「単相2線式」回路になります。
断線した線がないものと考えることができます。
つまり
以下のようになります。

そこで次は回路の合成抵抗を求めます。
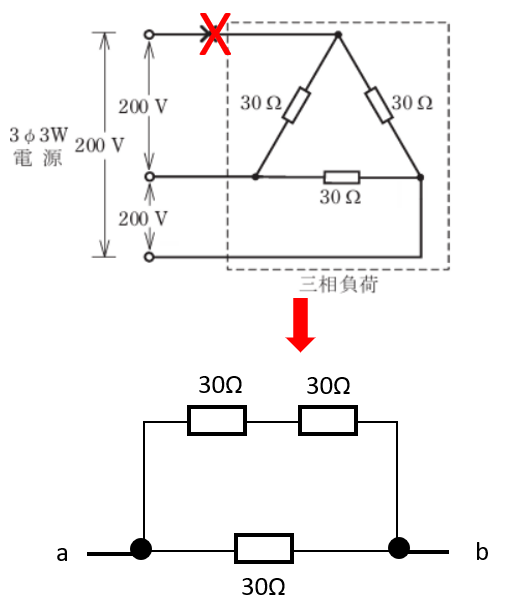
上の回路が30Ωと30Ωの直列接続になっています。
30 + 30 = 60Ω
つぎに30Ωが並列接続になっているので
60 x 30 / 60 + 30 = 1800 / 90 = 20Ω
です。
電圧Vが問題文より200Vとなっているので
オームの法則より
V = I R
I = V / R
=200 / 20 = 10[A]
になり
負荷の全消費電力Pは
P = I V = 10 x 200 = 2000W=2.0[kW]
になります。

【答え・二】

問題7

図のような単相3線式回路において，電線1線当たりの抵抗が0.2Ω のとき，a - b間の電圧[V]は。



• イ.96
• ロ.100
• ハ.102
• ニ.106

---

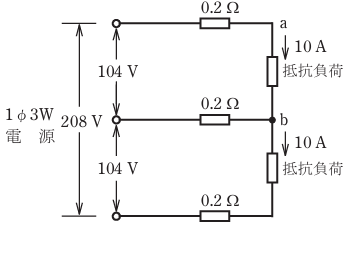
【解説】

まずポイントは負荷抵抗に流れる電流がともに10Aということで平衡しています。
この場合真ん中の線中性線には電流が流れないので0Aとすることができます。
つぎにa-b間の電源電圧が104Vになっています。
求めるa-b間の電圧は
204V - 電圧降下 = a-b間の電圧
となり
電圧降下の式で電圧降下を求めて行きます。
電圧降下=0.2 x 10 = 2V
104-2=102V
になります。

【答え・ハ】

問題8

低圧屋内配線の合成樹脂管工事で，管内に直径2.0 mmの600Vビニル絶縁電線(軟銅線)を4本収めて施設した場合，電線1本当たりの許容電流［A］は。
ただし，周囲温度は30℃以下とする。
• イ.17
• ロ.19
• ハ.22
• ニ.24

---

【解説】

この問題は以下のことを覚えておかなければなりません。

単線		より線
太さ	許容電流値	太さ	許容電流値
1.6[mm]	27[A]	2[mm2]	27[A]
2.0[mm]	35[A]	3.5[mm2]	37[A]
2.6[mm]	48[A]	5.5[mm2]	49[A]
3.2[mm]	62[A]	8[mm2]	61[A]
		14[mm2]	88[A]

問題文より管内に直径2.0 mmの600Vビニル絶縁電線(軟銅線)を4本収めて施設した場合
とあります。
単線直径2.0mmの許容電流は35[A]です。
次のポイントが
4本収めて施設した場合
とあり
これもまた次のことを覚えておかないといけません。

同一管内の電線数	電流減少係数
3本以下	0.70
4本	0.63
5本または6本	0.56

つまり今回は4本なので
35 x 0.63=22.05
になります。

【答え・ハ】

問題9

図のように定格電流50 Aの過電流遮断器で保護された低圧屋内幹線から分岐して，7 mの位置に過電流遮断器を施設するとき，a - b間の電線の許容電流の最小値［A］は。



• イ.12.5
• ロ.17.5
• ハ.22.5
• ニ.27.5

---

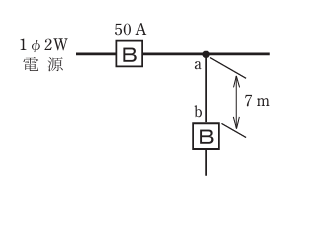
【解説】

分岐回路には、“原則として”幹線の分岐点から3m以内に「開閉器及び過電流遮断器」を設けなくてはなりません。
とありますが例外があります。
まず以下の表は覚えておいてください。

分岐点からの電線の許容電流が、幹線の許容電流の55%以上	制限なしに施設できる。
分岐点からの電線の許容電流が、幹線の許容電流の35%以上	分岐点から3m超8m以下に施設できる。
上記にあてはまらない場合	分岐点から3m以下に施設できる。

重要なポイントとして

• 分岐回路の過電流遮断器の施設位置が8mを越えるときは、0.55×過電流遮断器の定格電流とします。
• 分岐回路の過電流遮断器の施設位置が3mを越え8m以下のときは、0.35×過電流遮断器の定格電流とします。

となります。
幹線の定格電流は50Aです。
つぎにa-b間が7mです。
つまり
分岐回路の過電流遮断器の施設位置が3mを越え8m以下のときは、0.35×過電流遮断器の定格電流
になりますので
50 x 0.35=17.5[A]
になります。

【答え・ロ】

問題10

低圧屋内配線の分岐回路の設計で，配線用遮断器，分岐回路の電線の太さ及びコンセントの組合せとして，適切なものは。
ただし，分岐点から配線用遮断器までは3 m，配線用遮断器からコンセントまでは8 m とし, 電線の数値は分岐回路の電線(軟銅線)の太さを示す。 また，コンセント兼用コンセントではないものとする。

---

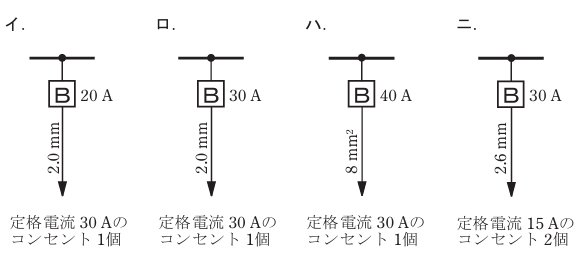
【解説】

この問題は以下の表を覚えておかないといけません。

分岐回路の種類	過電流遮断器の 定格容量	コンセントの 定格電流	電線太さの最小値
15[A]分岐回路	15[A]	15[A]以下	直径1.6mm以上(または2mm2以上)
B20[A]分岐回路 配線用遮断器	20[A]以下	20[A]以下	直径1.6mm以上(または2mm2以上)
20[A]分岐回路	20[A]のヒューズに限る	20[A]	直径2mm以上(または3.5mm2以上)
30[A]分岐回路	30[A]以下	20[A]～30[A]	直径2.6mm以上(または5.5mm2以上)
40[A]分岐回路	40[A]以下	30[A]～40[A]	断面積8mm2以上
50[A]分岐回路	50[A]以下	40[A]～50[A]	断面積8mm2以上

表をもとに順に見ていきます。
(イ)ですがB20Aの分岐回路となります。
電線の最小太さは、1.6㎜以上です。
コンセントの定格電流は、20A以下となっています。
問題のイでは電線の太さが2.0mmとなっているので、適切です。
つぎに
コンセントですが
コンセントの定格電流は、30Aとなっています。
コンセントは不適切です。
(ロ)ですが30Aの分岐回路となります。
電線の最小太さは、2.6㎜以上です。
コンセントの定格電流は、20A～30Aとなっています。
問題のロでは電線の太さが2.0mmとなっているので、不適切です。
コンセントの定格電流は、30Aとなっています。コンセントは、適切です。
(ハ)ですが40Aの分岐回路となります。
電線の最小太さは、断面積8mm²以上です。
問題のハですが電線の太さが8mm²となっているので、適切です。
コンセントの定格電流は、30Aとなっているので、適切です。
二ですが30Aの分岐回路となります。
問題の二では電線の最小太さは、2.6㎜以上です。
コンセントの定格電流は、20A～30Aとなっています。
電線の太さが2.6mmとなっているので、適切です。
コンセントの定格電流は、15Aとなってるので不適切です。
そこで電線の太さとコンセントの定格電流が両方とも適切なのはハです。

【答え・ハ】

Sponsored link