令和7年度上期
問題1
- 図のような回路で,スイッチS1を閉じ,スイッチS2を開いたときの,端子 間の合成抵抗[Ω]は。
- イ.45
- ロ.60
- ハ.75
- ニ.120
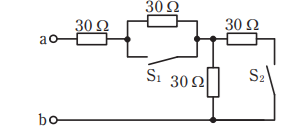
【解説】
問題よりスイッチS1を閉じスイッチS2を開いた時なので以下のようになります。
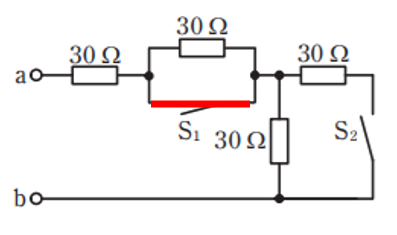
Siを閉じるとS1の部分が短絡状態になり、その上の30Ωには電流が流れません。
またS2を開いているのでその部分も電流が流れません。
従って電流は以下のように流れます。
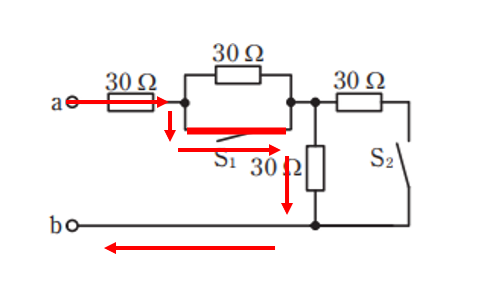
30 + 30 = 60Ω
になります。
【答え・ロ】
問題2
- 直径1.6 mm,長さ8 mの軟銅線と電気抵抗が等しくなる長さ32 mの軟銅線の直径[mm]
- イ.0.8
- ロ.2.0
- ハ.3.2
- ニ.6.4
ただし,軟銅線の抵抗率は同一とする。 は
【解説】
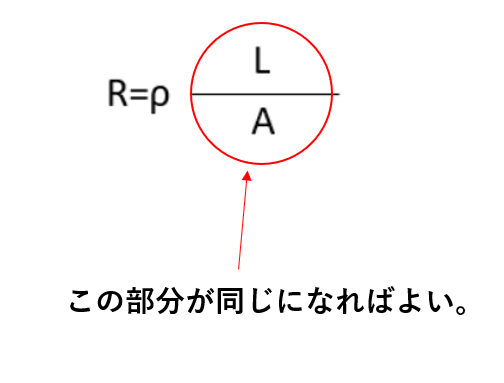
抵抗を求める公式は以下になります。
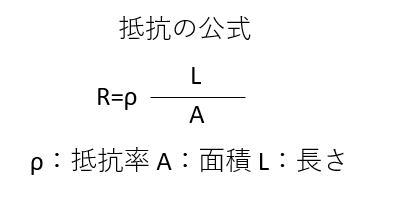
つまり
Aは断面積なので
]断面積を求める公式
直径 x 直径 x 3.14で求めることができます。
従って直径1.6mmの断面積は
1.6 x 1.6 x 3.14 = 80.384mm2
になります。
従って長さが8mなので以下のようになります。

【答え・ハ】
問題3
- 電線の接続不良により,接続点の接触抵抗が0.2Ω となった。この電線に10 Aの電流が流れると,接続点から1時間に発生する熱量[kJ]は。
- イ.72
- ロ.144
- ハ.288
- ニ.576
ただし,接触抵抗の値は変化しないものと する。
【解説】
熱量の公式で求めることができます。
熱量H=I2Rt
まずここでのtの単位は秒なので問題では1時間に発生する熱量を求めないといけません。
従って以下のように計算します。
1時間は
60 x 60 = 3600秒
H=102 x 0.2 x 3600 = 72000=72kJ
【答え・イ】
問題4
- 図のような交流回路で,電源電圧102 V,抵抗の両端の電圧が90 V,リアクタンスの両端の電圧が48 Vであるとき,負荷の力率[%]は。
- イ.47
- ロ.69
- ハ.88
- ニ.96
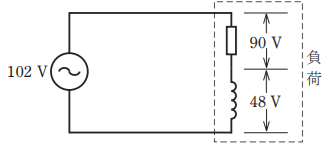
【解説】
この問題は電源電圧102 V,抵抗の両端の電圧が90 Vが分かっていますのでこの場合の力率は以下の公式で求めることができます。
力率cosΘ= VR / V x 100
cosΘ= 90 / 102 x 100 = 88.2%
【答え・ハ】
問題5
- 図のような三相 3 線式回路に流れる電流I [A]は。
- イ.8.3
- ロ.11.6
- ハ.14.3
- ニ.20.0
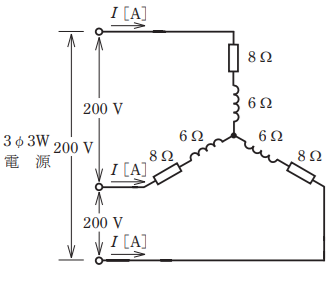
【解説】
この問題はスター結線です。
スター結線の場合は
線電流=相電流
線間電圧=√3 x 相電圧
問題より線間電圧200Vとなっているので
相電圧は以下のようになります。
200 = √3 x 相電圧
相電圧=200 / √3=115.6V
次に抵抗とコイルのインピーダンスを求めます。
抵抗が8Ωでコイルが6ΩなのでインピーダンスZは以下のようになります。
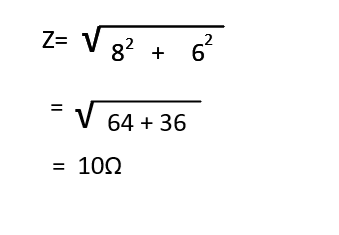
V = I x Z
I = V / Z=115.6 / 10 = 11.56 =11.6
【答え・ロ】
問題6
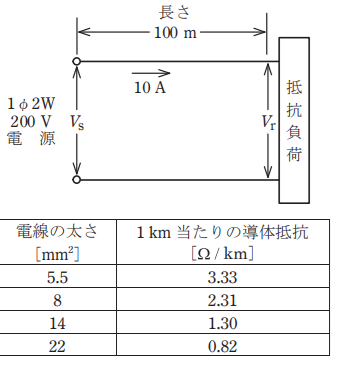
- 図のような単相2線式回路において,配線の長さは100 m,負荷電流は10 Aで,抵抗負荷が接続されている。配線の電圧降下 (Vs-Vr)を4 V以内にするための電線の最小太さ(断面積)[mm2]は。
- イ.5.5
- ロ.8
- ハ.14
- ニ.22
ただし,電線の抵抗は表のとおりとする。
【解説】
電圧降下の問題なので電圧降下の式を用いります。
- 単相2線式・・・2Ir
- 単相3線式・・・Ir
- 三相3線式・・・√3Ir
問題より配線の長さが100mです。
負荷電流が10A
順に計算をしていき電圧降下が4V以下になるものを探していかなければなりません。
電線の太さが5.5mm2の場合
1 km 当たりの導体抵抗は、3.33となっています。
従って100mの場合の導体抵抗は
3.33 x 0.1 = 0.333
になります。
電圧降下の式に代入すると
2 x 10 x 0.333=6.66V
になり4Vを超えていますので不適切になります。
電線の太さが8mm2の場合
1 km 当たりの導体抵抗は、2.31となっています。
従って100mの場合の導体抵抗は
2.31 x 0.1 = 0.231
になります。
電圧降下の式に代入すると
2 x 10 x 0.231=4.62V
になり4Vを超えていますので不適切になります。
電線の太さが14mm2の場合
1 km 当たりの導体抵抗は、1.30となっています。
従って100mの場合の導体抵抗は
1.30 x 0.1 = 0.130
になります。
電圧降下の式に代入すると
2 x 10 x 0.130=2.6V
になり4Vを超えていないので適切です。
電線の太さが22mm2の場合
1 km 当たりの導体抵抗は、0.82となっています。
従って100mの場合の導体抵抗は
0.82 x 0.1 = 0.082
になります。
電圧降下の式に代入すると
2 x 10 x 0.082=1.64V
になり4Vを超えていないので適切です。 ここで問題より電線の最小太さ(断面積)[mm2]
とあるので
最小はハの14mm2となります。
【答え・ハ】
問題7
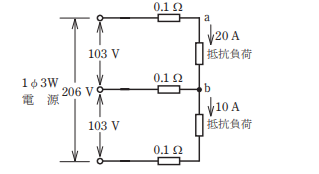
- 図のような単相3線式回路において,電線1線当たりの抵抗が0.1 Ωのとき,a-b 間の電圧[V]は。
- イ.99
- ロ.100
- ハ.101
- ニ.102
【解説】
この問題で気を付けるポイントは抵抗負荷が20Aと10Aあります。
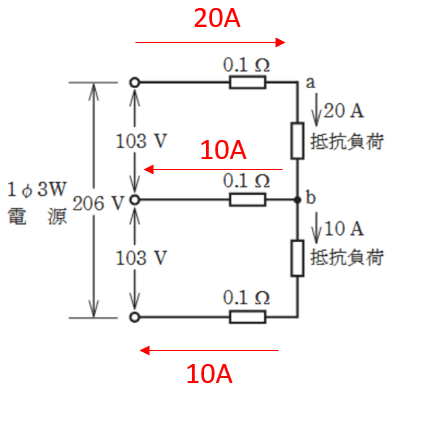
つまりこの回路は平衡負荷ではないので真ん中の中性線にも電流が流れるのでこのことを考慮して電圧降下を求めていかなければなりません。
- 単相2線式・・・2Ir
- 単相3線式・・・Ir
- 三相3線式・・・√3Ir
上の線の電圧降下は電流が20Aが流れており、電線の抵抗が0.1Ωです。
従って電圧降下は
20 x 0.1 = 2V
になります。
中性線には電流が10Aが流れており、電線の抵抗が0.1Ωです。
従って電圧降下は,br /> 10 x 0.1 = 1V
になり
a-b間の電源電圧が103Vなので
103-2-1=100V
になります。
【答え・ロ】
問題8
- 合成樹脂製可とう電線管(PF管)による低圧屋内配線工事で,管内に断面積5.5 mm2の600 Vビニル絶縁電線(軟銅線)3本を収めて施設した場合,電線1本当たりの許容電流[A]は。
- イ.26
- ロ.34
- ハ.42
- ニ.49
ただし,周囲温度は30℃以下,電流減少係数 は0.70とする。
【解説】
この問題は以下のことを覚えておかなければなりません。
| 単線 | より線 | ||
|---|---|---|---|
| 太さ | 許容電流値 | 太さ | 許容電流値 |
| 1.6[mm] | 27[A] | 2[mm2] | 27[A] |
| 2.0[mm] | 35[A] | 3.5[mm2] | 37[A] |
| 2.6[mm] | 48[A] | 5.5[mm2] | 49[A] |
| 3.2[mm] | 62[A] | 8[mm2] | 61[A] |
| 14[mm2] | 88[A] | ||
断面積5.5 mm2の許容電流値は49[A]です。
また問題より
電流減少係数は0.70となっています。
従って
49 x 0.70=34.3
になりますので最も近いロが正解です。
【答え・ロ】
問題9
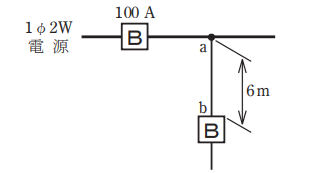
- 図のように定格電流100 Aの過電流遮断器で保護された低圧屋内幹線から分岐して,6 mの位置に過電流遮断器を施設するとき,a-b 間の電線の許容電流の最小値[A]は。
- イ.25
- ロ.35
- ハ.45
- ニ.55
【解説】
分岐回路には、“原則として”幹線の分岐点から3m以内に「開閉器及び過電流遮断器」を設けなくてはなりません。
とありますが例外があります。
まず以下の表は覚えておいてください。
| 分岐点からの電線の許容電流が、幹線の許容電流の55%以上 | 制限なしに施設できる。 |
| 分岐点からの電線の許容電流が、幹線の許容電流の35%以上 | 分岐点から3m超8m以下に施設できる。 |
| 上記にあてはまらない場合 | 分岐点から3m以下に施設できる。 |
重要なポイントとして
- 分岐回路の過電流遮断器の施設位置が8mを越えるときは、0.55×過電流遮断器の定格電流とします。
- 分岐回路の過電流遮断器の施設位置が3mを越え8m以下のときは、0.35×過電流遮断器の定格電流とします。
問題より幹線からの距離は、6mとなっています。
6mは
分岐回路の過電流遮断器の施設位置が3mを越え8m以下のときは、0.35×過電流遮断器の定格電流に該当します。
従って定格電流が100Aなので
100 x 0.35 = 35[A]
になります。
【答え・ロ】
問題10
低圧屋内配線の分岐回路の設計で,配線用遮断器,分岐回路の電線の太さ及びコンセントの組合せとして,適切なものは。
ただし,分岐点から配線用遮断器までは3 m,配線用遮断器からコンセントまでは8 m とし, 電線の数値は分岐回路の電線(軟銅線)の太さを示す。
また,コンセントは兼用コンセントではないものとする。

【解説】
この問題は以下の表を覚えておかないといけません。
| 分岐回路の種類 | 過電流遮断器の 定格容量 | コンセントの 定格電流 | 電線太さの最小値 |
|---|---|---|---|
| 15[A]分岐回路 | 15[A] | 15[A]以下 | 直径1.6mm以上(または2mm2以上) |
| B20[A]分岐回路 配線用遮断器 | 20[A]以下 | 20[A]以下 | 直径1.6mm以上(または2mm2以上) |
| 20[A]分岐回路 | 20[A]のヒューズに限る | 20[A] | 直径2mm以上(または3.5mm2以上) |
| 30[A]分岐回路 | 30[A]以下 | 20[A]~30[A] | 直径2.6mm以上(または5.5mm2以上) |
| 40[A]分岐回路 | 40[A]以下 | 30[A]~40[A] | 断面積8mm2以上 |
| 50[A]分岐回路 | 50[A]以下 | 40[A]~50[A] | 断面積8mm2以上 |
イは30Aの分岐回路です。
電線の最小太さは、2.6㎜以上(5.5㎜2以上)です。
コンセントの定格電流は、20~30Aとなっています。
問題のイですが電線の太さが2.0なので基準値を満たしていないので不適切です。
コンセントの定格電流は、20Aとなっているのでコンセントについては基準値を満たしています。
ロはB20Aの分岐回路です。
電線の最小太さは、1.6㎜以上(2mm2以上)です。 コンセントの定格電流は、20A以下となっています。
問題のロですが電線の太さが2.6mmとなっており、基準を満たしているので適切です。
しかしコンセントが30Aとなっており基準値を満たしていないので不適切です。
ハはイと同じく30Aの分岐回路です。
電線の最小太さは、2.6㎜以上(5.5㎜2以上)です。
コンセントの定格電流は、20~30Aとなっています。
問題のハですが電線の太さが5.5㎜2となっているので、基準を満たしているので適切です。
しかしコンセントの定格電流は、15Aとなっているので不適切です。
二はロと同じB20Aの分岐回路です。
電線の最小太さは、1.6㎜以上(2mm2以上)です。 コンセントの定格電流は、20A以下となっています。
電線の太さが2.0mmとなっていて、基準の「1.6㎜以上」を満たしているので適切です。
コンセントについても20A以下で基準を満たしているので適切です。
従って電線の太さとコンセントの定格電流が両方とも満たしている二が正しいです。
【答え・二】
Sponsored link





