電気入門
総合情報.com

電気の基礎入門及び電気工事士資格対策サイトです。

令和6年度下期

問題1

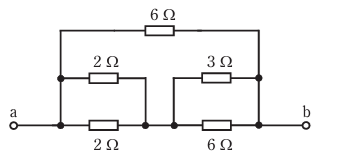
図のような回路で，端子a-b間の合成抵抗［Ω］は。



• イ.1
• ロ.2
• ハ.3
• ニ.4

---

【解説】

合成抵抗は次の順に求めていきます。
①2Ωと2Ωの並列回路
②3Ωと6Ωの並列回路
③①と②の直列回路
④③と6Ωの並列回路
まず①ですが
2 x 2 / 2 + 2 = 1Ω
②ですが
3 x 6 / 3 + 6 = 2Ω
③1 + 2 = 3Ω
④6 x 3 / 6 + 3 = 2Ω

【答え・ロ】

問題2

A，B 2本の同材質の銅線がある。Aは直径1.6 mm，長さ20 m，Bは直径3.2 mm，長さ 40 mである。Aの抵抗はBの抵抗の何倍か。
• イ.2
• ロ.3
• ハ.4
• ニ.5

---

【解説】

抵抗の公式は以下です。

この問題は同材質の銅線なので抵抗率ρは同じなので無視できます。
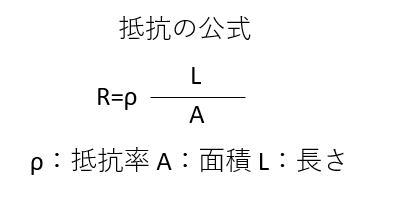
問題では直径になっていますので断面積に変換してやらなければなりません。
断面積(S) = 半径 X 半径 X　円周率
で求めることができますので
直径1.6mmの断面積は
0.8 x 0.8 x 3.14 = 2.0096
直径3.2mmの断面積は
1.6 x 1.6 x 3.14 = 8.0384
になりますので
それぞれ抵抗の公式に代入していきます。
直径1.6mmの抵抗は
R=ρ x 20/2.0096= 9.95ρ
直径3.2mmの抵抗は
R=ρ x 40/8.0384=4.976ρ
ここで材質がともの銅線なので抵抗率は同じになりますのでρは無視することができます。
9.95ρ / 4.976ρ = 1.999
従って2倍になります。

【答え・イ】

問題3

電線の接続不良により，接続点の接触抵抗が0.5Ω となった。この電線に20 Aの電流が流れると，接続点から1時間に発生する熱量［kJ］は。
ただし，接触抵抗の値は変化しないものとする。
• イ.72
• ロ.144
• ハ.720
• ニ.1440

---

【解説】

熱量の問題です。
熱量の公式は
H = P x t
です。
接触抵抗が0.5Ωで電線に20Aの電流が流れているので電力の公式
P=IV=I x I x R
より
P= 20 x 20 x 0.5=200W
になります。
熱量の公式のtは時間(秒)になります。
1時間に発生する熱量なので
1分は60秒だから
1時間は60分 x 60 秒=3600秒
になります。
H = 200 x 3600=720000J=720kJ
になります。

【答え・ハ】

問題5

定格電圧V［V］，定格電流I［A]の三相 誘導電動機を定格状態で時間 t［h］の間，連続運転したところ，消費電力量が W［kW・h］であった。この電動機の力率［％］を表す式は。
• イ.W/3VIt x 10⁵
• ロ.√3VI/Wt x 10⁵
• ハ.3VI/W x 10⁵
• ニ.W/√3VIt x 10⁵

---

【解説】

三相誘導電動機の消費電力は
P=√3VIcosθ x 10^-3
です。
消費電力量は
W=pt
W=P=√3VIcosθ x 10^-3x t
ここで、今回は力率を求めなければならないです。
ここで力率はcosθになるので上記式をcosθ=にしなければなりません。
cosθ=W x 10³ / √3VIt
となります。
しかし問題より%で求められているので
最後に
x10²
を忘れないようにしましょう。
答えは
cosθ=W/√3VIt×105
になります。

【答え・ニ】

問題6

図のような単相2線式回路で，c-c’間の電圧が99 Vのとき，a-a’間の電圧［V］は。
ただし，rは電線の抵抗［Ω］とする。



• イ.102
• ロ.103
• ハ.104
• ニ.105

---

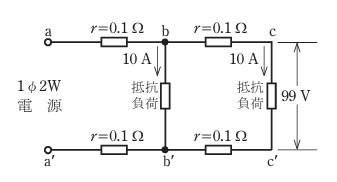
【解説】

この問題は分かりにくいですが電圧降下の問題です。
電圧降下の公式は
単相2線式・・・2Ir
単相3線式・・・Ir
三相3線式・・・√3Ir
です。
問題の問題でb-c間には、10Aの電流が流れています。 問題より
抵抗rは0.1Ωなので
2 x 10 x 0.1 = 2V
です。
bの電圧は
b-c間の電圧降下が2Vなので
bの電圧は99 + 2 = 101V
になります。
次にa-b間の電圧を求めると
a-b間には10+10=20A
の電流が流れています。
抵抗rは0.1Ωなので
2 x 20 x 0.1 = 4V
になります。
従って
101+4=105V になります。

【答え・ニ】

問題7

図1のような単相3線式回路を，図2のような単相2線式回路に変更した場合，配線の電力損失はどうなるか。
ただし，負荷電圧は100 V一定で，負荷A，負荷Bはともに消費電力1 kWの抵抗負荷で，電線の抵抗は1線当たり0.1 Ωとする。



• イ.1/4倍になる。
• ロ.1/2倍になる。
• ハ.2倍になる。
• ニ.4倍になる。

---

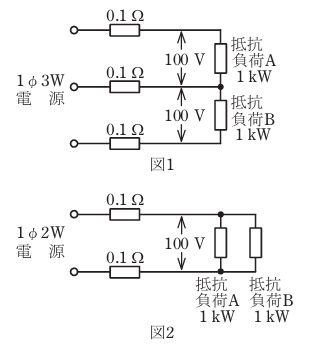
【解説】

電力損失の問題です。
電力損失の公式は以下になります。
電力損失の公式
単相2線式・・・2rI²
単相3線式・・・2rI²
三相3線式・・・3rI²
この問題は順に単相3線式回路と単相3線式回路の電力損失を求めて比較してやる必要があります。
では、上の回路単相3線式回路から電力損失を計算していきます。
この問題では抵抗負荷Aと抵抗負荷Bがともに1kWですので平衡していることになり中性線には電流が流れません。
つまり0Aです。
従って
単相3線式・・・2rI²
に値を代入すると
2 x 0.1 x 10 x 10 = 20W
次に単相2線式を計算していきます。
抵抗負荷Aに流れる電流は
負荷が1kw=1000wで電圧が100Vなので
電力の公式
P=IV
より
1000 = I x 100
I = 10A
抵抗負荷Bも同じく10Aです。
従って
単相2線式には20Aの電流が流れています。
単相2線式回路の電力損失は、2rI²より
2 x 0.1 x 20 x 20 = 80W
となり
80/20=4倍
になります。

【答え・ニ】

問題8

金属管による低圧屋内配線工事で，管内に断面積5.5mm²の600Vビニル絶縁電線(軟銅線)4本を収めて施設した場合，電線1本当たりの許容電流［A］は。
ただし，周囲温度は30 ℃以下，電流減少係数は0.63とする。
• イ.19
• ロ.24
• ハ.31
• ニ.49

---

【解説】

この問題は以下のことを覚えておかなければなりません。

単線		より線
太さ	許容電流値	太さ	許容電流値
1.6[mm]	27[A]	2[mm2]	27[A]
2.0[mm]	35[A]	3.5[mm2]	37[A]
2.6[mm]	48[A]	5.5[mm2]	49[A]
3.2[mm]	62[A]	8[mm2]	61[A]
		14[mm2]	88[A]

管内に断面積5.5mm²の600Vビニル絶縁電線(軟銅線)4本を収めて施設した。
とあります。
断面積5.5mm²の許容電流値は49Aです。
また、電流減少係数は0.63とする。
とあるので
49 x 0.63=30.87

【答え・ハ】

Sponsored link