令和6年度上期
問題1
- 図のような回路で,8 Ωの抵抗での消費電力[W]は。
- イ.200
- ロ.800
- ハ.1200
- ニ.2000
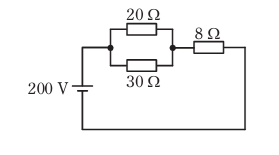
【解説】
まず電圧200Vと分かっているので回路の合成抵抗を求めたらオームの法則により回路に流れる電流が求めることができます。
合成抵抗は以下のように求めます。
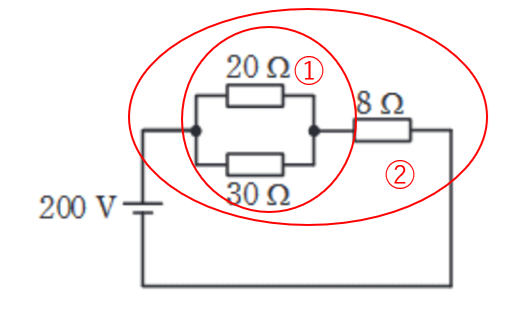
20 x 30 / 20 + 30 = 12Ω
①の12Ωと8Ωの直列回路です。
12+8=20Ωです。
合成抵抗が20Ωなのでオームの法則
V = IR
より
200 = I x 20
I = 10A
8Ωの抵抗の消費電力は電力の公式
P=IV=I x I x R=10 x 10 x 8 = 800W
になります。
【答え・ロ】
問題3
- 電線の接続不良により,接続点の接触抵抗が 0.2Ω となった。この電線に 15 A の電流が流れると,接続点から 1 時間に発生する熱量[kJ]は。
- イ.11
- ロ.45
- ハ.72
- ニ.162
ただし,接触抵抗の値は変化しないものとする
【解説】
熱量を求める問題です。
熱量を求める公式は
H = P x t
接触抵抗が0.2Ωで電流が15A流れているので電力を求める公式
P = I x V=I x I x R
で求めることができます。
P=15 x 15 x 0.2 = 45W
次にtですがこれは時間(秒)になります。
問題で1時間とあります。
1時間を秒に直すと
1分=60秒
1時間は60分 x 60秒=3600秒
になるので
熱量Hは
H=45 x 3600 = 162000J=162kJ
になります。
【答え・ニ】
問題4
- 定格電圧V[V],定格電流I[A]の三相誘導電動機を定格状態で運転したところ,消費電力がP[kW]であった。この電動機の力率[%]を表す式は。
- イ.P/√3VI x 105
- ロ.√3P/VI x 105
- ハ.√3VI/P x 105
- ニ.VI/√3P x 105
【解説】
三相誘導電動機の消費電力は
P=√3VIcosθ×10-3
です。
今回の問題は力率を求めなければなりません。ここでの力率はcosθのことです。
従って
三相誘導電動機の消費電力の式をcosθ=の形に変換してやらなければなりません。
P=√3VIcosθ×10-3
cosθ=(P/√3VI) x 103
問題では%で求めなければいけないので
cosθ=(P/√3VI) x 103 X 102
になり
cosθ=(P/√3VI) x 105
になります。
【答え・イ】
問題5
- 図のような三相3 線式回路に流れる電流 I[A]は。
- イ.8.3
- ロ.11.6
- ハ.14.3
- ニ.20.0
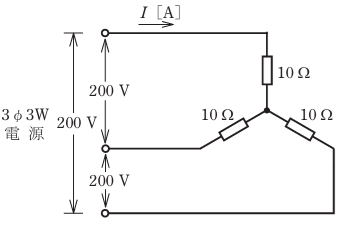
【解説】
問題はスター結線(Y結線)で線電流を求める問題です。
スター結線の場合は以下のことは必ず覚えておかなければなりません。
線電流=相電流
線間電圧=√3相電圧
つまり今回の問題は相電流を求めれば線電流も求められます。
回路図より線間電圧が200Vなので
相電圧は
200 = √3 x 相電圧
相電圧=200/√3
相電圧=115.6V
になります。
抵抗が10Ωなので
オームの法則
V=IR
より
115.6 = I x 10
I=11.56A
相電流が11.56A
になるので
線電流も11.56Aになります。
【答え・ロ】
問題6
- 図のように,電線のこう長8 mの配線により,消費電力2 000 Wの抵抗負荷に電力を供給した結果,負荷の両端の電圧は100 Vであった。配線における電圧降下[V]は。
- イ.1
- ロ.2
- ハ.3
- ニ.4
ただし,電線の電気抵抗は長さ1 000 m当たり3.2 Ωとする。
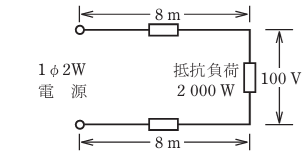
【解説】
電圧降下の問題なので、電圧降下の公式を使います。
電圧降下の公式
単相2線式・・・2Ir
単相3線式・・・Ir
三相3線式・・・√3Ir
問題より消費電力2000Wで電圧が100Vとなっているので
電流を求めることができます。
電力の公式
P=IV
より
2000 = I x 100
I = 20A
次に問題文より
電線の電気抵抗は長さ1 000 m当たり3.2 Ωとする。
とあります。
つまり
1000mで3.2Ωなので
1m当たりはその1/1000になることになります。
従って
1m当たりの抵抗は
3.2/1000=0.0032Ωになります。
問題では8mの配線なので
8 x 0.0032=0.0256Ω
になります。
問題では単相2線式なので
2Ir
で求めます。
2 x 20 x 0.0256=1.024V
になります。
【答え・イ】
問題7
- 図のような単相3線式回路において,電線1線当たりの抵抗が0.1 ,抵抗負荷に流れる電流がともに15 Aのとき,この配線の電力損失[W]は。
- イ.45
- ロ.60
- ハ.90
- ニ.135

【解説】
電力損失の問題なので電力損失の公式を使います。
電力損失の公式
単相2線式・・・2rI2
単相3線式・・・2rI2
三相3線式・・・3rI2
まずこの回路を見て抵抗負荷Aと抵抗負荷Bがともに15Aなので
この回路は平衡していることになり
中性線には電流が流れません。つまり中性線は0Aです。
回路図より
抵抗が01Ω
電流が15Aであることがわかります。
この回路は単相3線式なので
2rI2
より
2 x 0.1 x 15 x 15=45V
【答え・イ】
問題8
- 金属管による低圧屋内配線工事で,管内に直径2.0 mmの600Vビニル絶縁電線(軟銅線)4本を収めて施設した場合,電線1本当たりの許容電流[A]は。
- イ.17
- ロ.22
- ハ.30
- ニ.35
ただし,周囲温度は30 ℃以下,電流減少係数は0.63とする。
【解説】
この問題は以下のことを覚えておかなければなりません。
| 単線 | より線 | ||
|---|---|---|---|
| 太さ | 許容電流値 | 太さ | 許容電流値 |
| 1.6[mm] | 27[A] | 2[mm2] | 27[A] |
| 2.0[mm] | 35[A] | 3.5[mm2] | 37[A] |
| 2.6[mm] | 48[A] | 5.5[mm2] | 49[A] |
| 3.2[mm] | 62[A] | 8[mm2] | 61[A] |
| 14[mm2] | 88[A] | ||
直径2.0 mmの600Vビニル絶縁電線(軟銅線)4本を収めて施設した場合
とあります。
直径2.0mmのときの許容電流値は35Aとなっています。
また、電流減少係数は0.63とする。
となっているので
35 x 0.63=22.05
【答え・ロ】
問題9
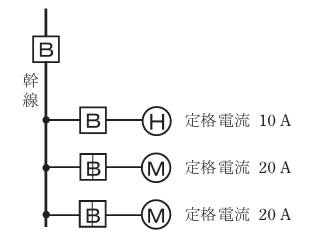
- 図のような電熱器H 1台と電動機M 2台が接続された単相2線式の低圧屋内幹線がある。この幹線の太さを決定する根拠となる電流IW[A]と幹線に施設しなければならない過電流遮断器の定格電流を決定する根拠となる電流IB[A]の組合せとして,適切なものは。
- イ.IW 50
IB 125 - ロ.IW 50
IB 130 - ハ.IW 60
IB 130 - ニ.IW 60
IB 150
ただし,需要率は100%とする。
【解説】
この問題は以下のことを覚えておかなければいけません。
幹線に求められる許容電流
幹線の許容電流(電流の太さ)は、負荷の定格電流の場合よって決まります。
特に負荷に電動機は始動するときに大きな電流が流れるため、余裕をもって許容電流を決めなければいけません。
電動機の定格電流が小さい場合
電動機の定格電流の総量IMが、その他の負荷の定格電流の総量IHより小さいか等しい場合は以下のように幹線の許容電流は決まります。
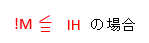
幹線の許容電流はIWは
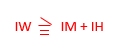
になります。
電動機の定格電流が大きい場合
電動機の定格電流の総量IMが、その他の負荷の定格電流の総量IBより大きい場合は、以下のように幹線の許容電流は決まります。
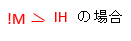
幹線の許容電流はIWは

になります。
まず問題文より電熱器(H)が1台、電動機(M)が2台ある。となっています。
まず電動機(M)は、定格電流20Aが2台あります。
従って
IM=20 + 20 = 40
になります。
今回は需要率が100%なのでそのままの数値が適用されます。
次に
電熱器(IH)は定格電流が10Aです。
従って
IH=10
になります。
ここからが少し難しくなります。
IMとIHの比較してやります。 IM=40
IH=10
だったので
比較すると
IM > IH
になります。 IM=40
なので
IM≦50A
に該当することになり
幹線の許容電流の公式は、「IW≧1.25IM+IH」になります。
IM=40
IH=10
なので
IW≧1.25IM+IH
IW≧1.25 x 40+10
IW≧50+10
IW≧60
従って
IW=60
が最小値になります。
また、この問題は電動機があるので
電動機がある場合は
2.5IWと3IM+IH
の数を比較します。
IM=40
IH=10
IW=60
より
2.5IW=2.5 x 60=150
3IM+IH=3 x 40 + 10=130
従って
2.5IW≧3IM+IH
は150≧130
になり
IB=130
となります。
従って
IW =60
IB =130 になります。
【答え・ハ】
Sponsored link





