令和5年度上期午後
問題1
- 図のような回路で,端子a-b間の合成抵抗[Ω]は。
- イ.1.1
- ロ.2.5
- ハ.6
- ニ.15
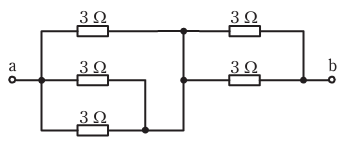
【解説】
合成抵抗は以下の順に①~④で求めていきます。
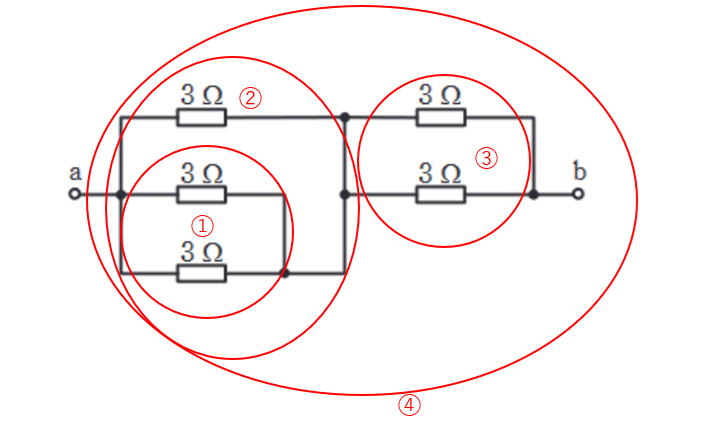
3 x 3/3 + 3=1.5Ω
②①の1.5Ωと3Ωの並列回路
1.5 x 3/1.5 + 3 = 4.5/4.5=1Ω
③3Ωと3Ωの並列回路
3 x 3/3 + 3=1.5Ω
④②の1Ωと③の1.5Ωの直列回路
1Ω + 1.5Ω=2.5Ω
【答え・ロ】
問題2
- A,B 2 本の同材質の銅線がある。Aは直径1.6mm,長さ100m,Bは直径3.2mm,長さ50mである。Aの抵抗はBの抵抗の何倍か。
- イ.1
- ロ.2
- ハ.4
- ニ.8
【解説】
抵抗を求める公式は以下になります。
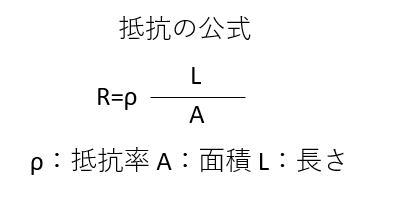
断面積(S) = 半径 X 半径 X 円周率
で求めることができますので
直径1.6mmの断面積は
0.8 x 0.8 x 3.14 = 2.0096
直径3.2mmの断面積は
1.6 x 1.6 x 3.14 = 8.0384
になりますので
それぞれ抵抗の公式に代入していきます。
直径1.6mmの抵抗は
R=ρ x 100/2.0096= 49.76ρ
直径3.2mmの抵抗は
R=ρ x 50/8.0384=6.22ρ
ここで材質がともの銅線なので抵抗率は同じになりますのでρは無視することができます。
49.76 / 8.0384 = 8
従って8倍になります。
【答え・ニ】
問題3
- 抵抗に15 Aの電流を1時間30分流したとき,電力量が4.5 kW・hであった。抵抗に加えた電圧[V]は。
- イ.24
- ロ.100
- ハ.200
- ニ.400
【解説】
問題で抵抗に 15 A の電流を 1 時間 30 分流したとき,電力量が 4.5 kW・h であった。」とあります。
そこで
単位のkW・h は電力量(消費電力量)の単位で、1kWの電力を1時間使用した場合の電力量が1kWhを意味します。
従って
1 時間 30 分で使用した電気量が4.5 kW・hになります。
1 時間 30 分は1.5hにるので
電力量4.5 kW・hを1.5hで割ると
3kWになります。
電力の公式
P = I V
より
3kW = 15 x V
V= 3000 / 15 = 200V
になります。
【答え・】
問題4
- 単相交流回路で200 Vの電圧を力率90%の負荷に加えたとき,15 Aの電流が流れた。負荷の消費電力[kW]は。
- イ.2.4
- ロ.2.7
- ハ.3.0
- ニ.3.3
【解説】
消費電力の公式は
P=VIcosθ
です。
cosθは力率のことで力率90%は0.9で計算していきます。
公式に代入すると
P= 15 x 200 x 0.9=2700W=2.7kW
になります。
【答え・ロ】
問題5
- 図のような三相 3 線式回路に流れる電流I[A]は。
- イ.8.3
- ロ.11.6
- ハ.14.3
- ニ.20.0
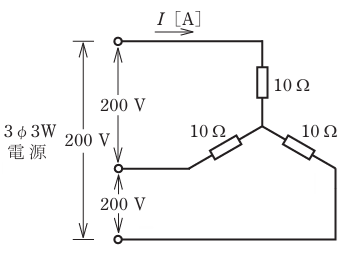
【解説】
この回路はスター結線(Y結線)です。
スター結線の場合は以下のことを覚えておかなければなりません。
線電流=相電流
線間電圧=√3 x 相電圧
回路図より線間電圧は、200Vであることがわかります。
線間電圧=√3 x 相電圧
より
200= √3 x 相電圧
相電圧= 200/√3
√3は1.73なので
相電圧= 200 / 1.73
=115.6V
負荷の抵抗が10Ωなので
オームの法則
V=IR
より
115.6 = I x 10
I=115.6 / 10 = 11.56A
になります。
スター結線の場合は
線電流=相電流
なので
3 線式回路に流れる電流I[A]も相電流と同じ
11.56A
になります。
【答え・ロ】
問題6
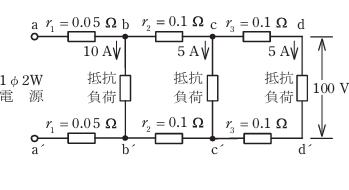
- 図のような単相 2 線式回路において,d-d' 間の電圧が100 Vのとき 間の電圧[V]は。
- イ.102
- ロ.103
- ハ.104
- ニ.105
ただし,r1 ,r2 及び r3は電線の電気抵抗[Ω]とする。
【解説】
電圧降下の問題なので電圧降下の式を用いります。
単相2線式・・・2Ir
単相3線式・・・Ir
三相3線式・・・√3Ir
まず順番に電圧降下を見ていきます。
右側の回路を見ていきます。
抵抗は0.1Ωです。
電流は5Aの単相2線式なので
2 x 5 x 0.1 = 1V
になります。
次に真ん中の回路を見ていきます。
抵抗は0.1Ωです。
電流は5 + 5 = 10Aです。
同じく単相2線式なので
2 x 10 x 0.1 = 2V
になります。
最後に左側回路を見ていきます。
抵抗は0.05Ωです。
電流は5 + 5 + 10 = 20Aです。
同じく単相2線式なので
2 x 20 x 0.05 = 2V
になります。
これらの電圧降下の合計がこの回路の電圧降下になります。
従って
1 + 2 + 2 = 5V
となります。
従ってa点の電圧は
100 + 5 = 105V
になります。
【答え・ニ】
問題7
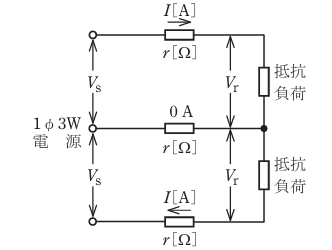
- 図のような単相3線式回路で,電線1線当たりの抵抗がr[Ω],負荷電流がI[A],中性線に流れる電流が0 Aのとき,電圧降下(Vs-Vr)[V]を示す式は。
- イ.2rI
- ロ.3rI
- ハ.rI
- ニ.√3rI
【解説】
電圧降下の問題なので電圧降下の式を用いります。
単相2線式・・・2Ir
単相3線式・・・Ir
三相3線式・・・√3Ir
問題の回路図より中性線に流れる電流は0Aとなっています。
つまり2つの抵抗負荷は平衡しています。
この問題は単相3線式なので電圧降下の公式は
rI
になります。
【答え・ハ】
問題8
- 低圧屋内配線工事に使用する600 Vビニル絶縁ビニルシースケーブル丸形(軟銅線),導体の直径2.0 mm,3心の許容電流[A]は。
- イ.19
- ロ.24
- ハ.33
- ニ.35
ただし,周囲温度は30 ℃以下,電流減少係数は0.70とする。
【解説】
この問題は以下のことを覚えておかなければなりません。
| 単線 | より線 | ||
|---|---|---|---|
| 太さ | 許容電流値 | 太さ | 許容電流値 |
| 1.6[mm] | 27[A] | 2[mm2] | 27[A] |
| 2.0[mm] | 35[A] | 3.5[mm2] | 37[A] |
| 2.6[mm] | 48[A] | 5.5[mm2] | 49[A] |
| 3.2[mm] | 62[A] | 8[mm2] | 61[A] |
| 14[mm2] | 88[A] | ||
したがって直径2.0mmの許容電流値は35Aとあります。
また、電流減少係数は0.70とあるので
35 x 0.7 = 24.5A
になります。
【答え・ロ】
Sponsored link





