電気入門
総合情報.com

電気の基礎入門及び電気工事士資格対策サイトです。

令和5年度上期午前

問題1

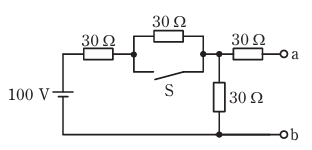
図のような回路で，スイッチSを閉じたとき，a - b 端子間の電圧［V］は。



• イ.30
• ロ.40
• ハ.50
• ニ.60

---

【解説】

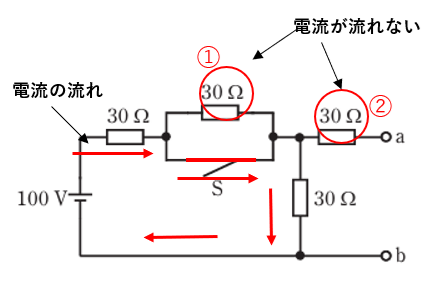
スイッチSを閉じたら①には電流が流れません。
また②にはそもそもaとbが閉じられていないので電流は流れません。
従ってスイッチSを閉じたら以下のようになります。

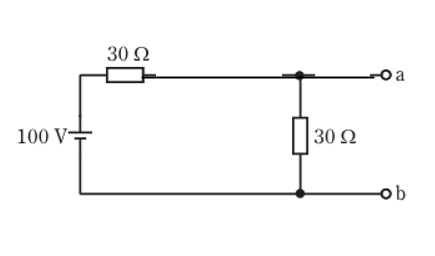
電圧は、「100V」で、30Ωを2つに分圧しているので
50Vになります。

【答え・ハ】

問題3

抵抗に100 Vの電圧を2時間30分加えたとき，電力量が4kW・hであった。抵抗に流れる電流［A］は。
• イ.16
• ロ.24
• ハ.32
• ニ.40

---

【解説】

問題文より抵抗に 100 V の電圧を 2 時間 30 分加えたとき，電力量が 4 kW・h であったとあります。
単位の kW・hは、電力量の単位で、１kWの電力を1時間使用した場合の電力量が１kW・hです。
2 時間 30 分で使用した電力量が4 kW・hです。
2 時間 30 分は2.5hになるので
4/2.5=1.6kWになり1600Wです。
電力の公式
P=VI
より
電圧は100Vなので
1600 = 100 x I
I=16A
になります。

【答え・イ】

問題4

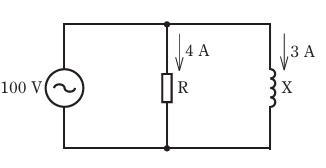
図のような回路で，抵抗Rに流れる電流が4 A，リアクタンスXに流れる電流が3 Aであるとき，この回路の消費電力［W］は。



• イ.300
• ロ.400
• ハ.500
• ニ.700

---

【解説】

消費電力は、抵抗で消費される有効電力なので
電力の公式より求めることができます。
P=VI
P = 100 x 4 = 400

【答え・ロ】

問題5

図のような三相3線式回路の全消費電力［kW］は。



• イ.2.4
• ロ.4.8
• ハ.9.6
• ニ.19.2

---

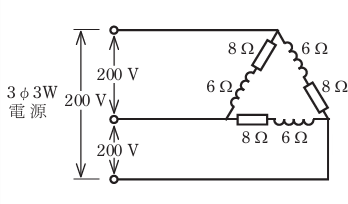
【解説】

1相分のインピーダンスZは

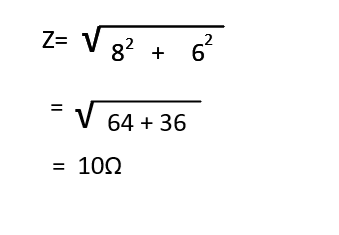
Z=10Aから、相電流を求めると 200 = I x 10
I=20A
になります。
P=I²R
より
P=20 x 20 x 8 = 3200W
これは1相分なので3相分の消費電力を求めるために3倍します。
3 x 3200=9600=9.6[kW]
消費電力を求めているので抵抗負荷のみで計算しなければなりません。

【答え・ハ】

問題6

図のような三相3線式回路で，電線1線当たりの抵抗が0.15Ω，線電流が10 Aのとき，この配線の電力損失［W］は。



• イ.15
• ロ.26
• ハ.30
• ニ.45

---

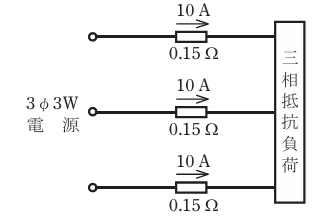
【解説】

三相3線式回路の電力損失を問う問題です。
電力損失の公式で求めることができますので公式は暗記しておきましょう。

• 単相2線式・・・・2rI²
• 単相3線式・・・・2rI²
• 三相3線式・・・・3rI²

問題文より式に代入すると
3 x 0.15 x 10 x 10 = 45W
今回は電流が線電流なので3を掛けましたが相電流の場合は少し異なるので気を付けましょう。

【答え・ニ】

問題7

図1のような単相2線式回路を，図2のような単相3線式回路に変更した場合，配線の電力損失はどうなるか。
ただし，負荷電圧は100 V一定で，負荷A，負荷Bはともに消費電力1kWの抵抗負荷で，電線の抵抗は1線当たり0.2Ωとする。



• イ.0になる。
• ロ.小さくなる。
• ハ.変わらない。
• ニ.大きくなる。

---

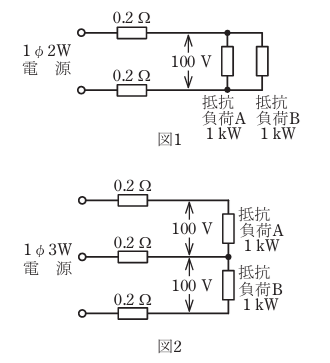
【解説】

電力損失の問題です。
従って電力損失の公式を使用します。

• 単相2線式・・・2rI²
• 単相3線式・・・2rI²
• 三相3線式・・・3rI²

まず単相2線式回路から計算します。
抵抗負荷Aに流れる電流は
電力1kW=1000W
電圧は100Vより
電力の公式
P=VI
より
1000 = 100 x I
I=10A
になります。
抵抗負荷Bにも同じく10Aが流れます。
抵抗負荷A + 抵抗負荷B=10 + 10 =20A
が流れます。
単相2線式の電力損失の公式より
単相2線式・・・2rI²
抵抗は問題文より
0.2Ωとあるので
2 x 0.2 x 20 x 20=160W
になります。
次に単相3線式回路を計算していきます。
抵抗負荷1kwには、10Aの電流が流れます。
この回路は抵抗負荷Aと抵抗負荷Bがともに1kWで平衡しているので
真ん中の中性線には電流は流れません。
単相3線式の電力損失の公式より
単相3線式・・・2rI²
抵抗は、問題文から0.2Ωとあるので
2 x 0.2 x 10 x 10=40W
となります。
単相2線式回路の電力損失は、160wで単相3線式回路の電力損失は、40Wですので答えは小さくなる。

【答え・ロ】

問題8

合成樹脂製可とう電線管PF管による低圧屋内配線工事で，管内に断面積5.5mm²の600Vビニル絶縁電線軟銅線7本を収めて施設した場合，電線1本当たりの許容電流［A］は。
ただし，周囲温度は30℃以下，電流減少係数は0.49とする。
• イ.13
• ロ.17
• ハ.24
• ニ.29

---

【解説】

この問題は以下のことを覚えておかなければなりません。

単線		より線
太さ	許容電流値	太さ	許容電流値
1.6[mm]	27[A]	2[mm2]	27[A]
2.0[mm]	35[A]	3.5[mm2]	37[A]
2.6[mm]	48[A]	5.5[mm2]	49[A]
3.2[mm]	62[A]	8[mm2]	61[A]
		14[mm2]	88[A]

問題文より
断面積5.5mm²の電線を「7本」収めて施設する、とあります。
つまり
断面積5.5mm²の許容電流は上の表より49Aとあります。
また、 電流減少係数は 0.49とあるので
49 x 0.49 = 24

【答え・ハ】

Sponsored link