電気入門
総合情報.com

電気の基礎入門及び電気工事士資格対策サイトです。

令和4年度下期午前

問題1

図のような直流回路に流れる電流I［A］は。



• イ.1
• ロ.2
• ハ.4
• ニ.8

---

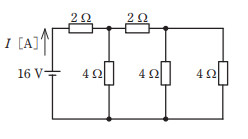
【解説】

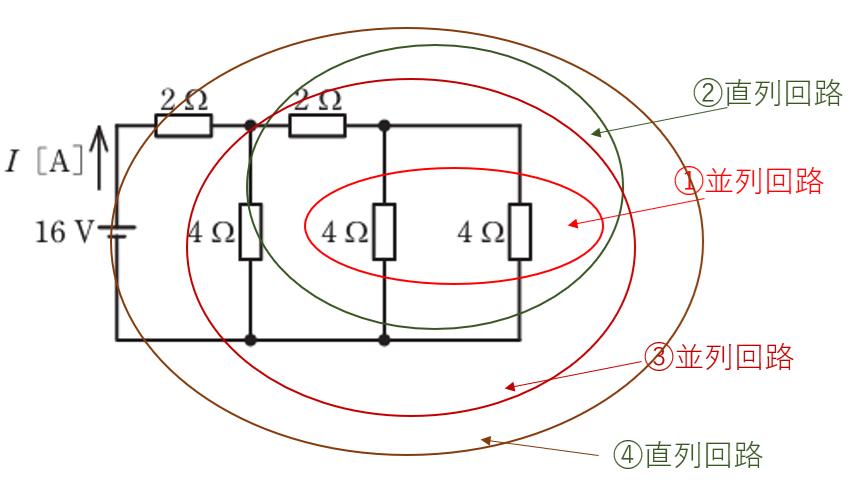
まず合成抵抗を求めます。
求め方は右側の回路から求めていきます。

• ①4Ωと4Ωの並列回路
• ②①と2Ωの直列回路
• ③②と4Ωの並列回路
• ④③と2Ωの直列回路

の順に求めます。
①4Ωと4Ωの並列回路は
4 x 4/4+4=16/8=2Ω
②2Ωと2Ωの直列回路は
2 + 2=4Ω
③4Ωと4Ωの並列回路は
4 x 4/4+4=16/8=2Ω
④2Ωと2Ωの直列回路は
2 + 2=4Ω
従ってこの回路の合成抵抗は4Ωになります。

あとはオームの法則で電流を求めます。
V=IR
16=I x 4
I=4A

【答え・ハ】

問題3

電熱器により，90kgの水の温度を20K上昇させるのに必要な電力量［kW・h］は。
ただし，水の比熱は4.2kJ/(kg・K)とし，熱効率は100％とする。
• イ.0.7
• ロ.1.4
• ハ.2.1
• ニ.2.8

---

【解説】

そのまま計算すればとけると思います。
問題文より

• 90kgの水の温度を20K上昇させる
• 水の比熱は4.2kJ/(kg・K)
• 熱効率は100％

とあるので
90 x 20 x 4.2=7560[kJ]です。電力量の単位がhになっているので1時間での電力量です。
7560kJは秒の単位なので
1時間＝60 x 60=3600秒ですので
7560/3600=2.1kW・h

【答え・ハ】

問題4

図のような交流回路において，抵抗12Ωの両端の電圧V［V］は。



• イ.86
• ロ.114
• ハ.120
• ニ.160

---

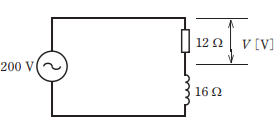
【解説】

回路のインピーダンスZは

になります。
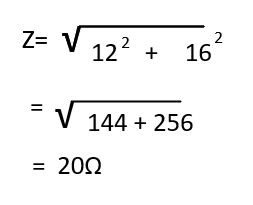
オームの法則
V=IR
ですがRをインピーダンスZに置き換えて
V=IZ
で計算します。
200 = I x 20
I=10A
になります。
V=10 x 12=120V
になります。

【答え・ハ】

問題5

図のような電源電圧E［V］の三相3線式回路で，図中の?印点で断線した場合，断線後のa-c間の抵抗R［Ω］に流れる電流I［A］を示す式は。



• イ.

  

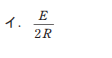
• ロ.

  

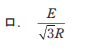
• ハ.

  

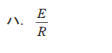
• ニ.

  

---

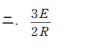
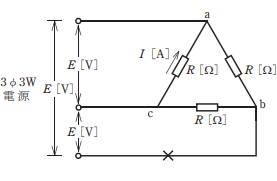
【解説】

一番下のところが断線したわけですから、回路図は以下のようになります。

a-c間の電流はオームの法則より
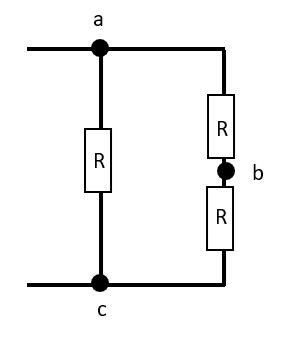
V＝IR
より
I= V/R
今回はE [V]となっているので
I= E/R
となります。

【答え・ハ】

問題6

図のような単相2線式電線路において，線路の長さは50m，負荷電流は25Aで，抵抗負荷が接続されている。線路の電圧降下(Vs-Vr)を4V以内にするための電線の最小太さ(断面積)［mm²］は。
ただし，電線の抵抗は表のとおりとする。



• イ.5.5
• ロ.8
• ハ.14
• ニ.22

---

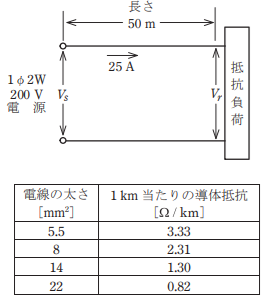
【解説】

単相2線式回路なので電圧降下を求める式は
V=2Irとなります。
電線太さ5.5mm²から計算します。
1km当たりの導体抵抗（Ω/km）は3.33となっています。
電線の長さは、50mなので
抵抗rは
50 x 3.33/1000=0.1665Ω
となります。
負荷電流Iは問題文より25Aとなっています。
電圧降下の公式
V=2Ir
に代入すると
V=2 x 25 x 0.1665=8.325V
になります。
問題より電圧降下を4V以内にしたいとのことなので
電線太さ5.5mm²を使用した場合は8.325Vになり不適切になります。

この要領で他の電線も計算していきます。
電線太さ8mm²を計算すると
1km当たりの導体抵抗（Ω/km）は2.31となっています。
抵抗rは
50 x 2.31/1000=0.1155Ω
となります。
V=2 x 25 x 0.1155=5.775V
になります。
電線太さ8mm²を使用した場合は5.775Vになり不適切になります。

電線太さ14mm²を計算すると
1km当たりの導体抵抗（Ω/km）は1.3となっています。
抵抗rは
50 x 1.3/1000=0.065Ω
となります。
V=2 x 25 x 0.065=3.25V
になります。
電線太さ14mm²を使用した場合は3.25Vになり4V以内になり適切な解答になります。

電線太さ22mm²を計算すると
1km当たりの導体抵抗（Ω/km）は0.82となっています。
抵抗rは
50 x 0.82/1000=0.041Ω
となります。
V=2 x 25 x 0.041=2.05V
になります。
電線太さ22mm²を使用した場合は2.05Vになり4V以内になり適切な解答になります。
正しいのは電線太さ14mm²と電線太さ22mm²
になりますが問題文より電線の最小太さ(断面積)となっているのでハの電線太さ14mm²
になります。

【答え・ハ】

問題7

図のような単相3線式回路において，電線1線当たりの抵抗が0.1Ω，抵抗負荷に流れる電流がともに15Aのとき，この電線路の電力損失［W］は。



• イ.23
• ロ.39
• ハ.45
• ニ.68

---

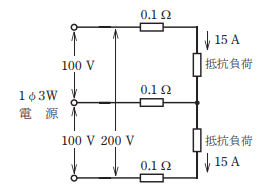
【解説】

電力損失の問題です。
電力損失も公式を使います。

• 単相2線式・・・2rI²
• 単相3線式・・・2rI²
• 三相3線式・・・3rI²

ここでは単相3線式回路の問題です。
2 x 0.1 x 15 x 15=45

【答え・ハ】

問題8

金属管による低圧屋内配線工事で，管内に直径1.6mmの600Vビニル絶縁電線(軟銅線)3本を収めて施設した場合，電線1本当たりの許容電流［A］は。
ただし，周囲温度は30℃以下，電流減少係数は0.70とする。
• イ.19
• ロ.24
• ハ.27
• ニ.34

---

【解説】

この問題は以下のことを覚えておかなければなりません。

単線		より線
太さ	許容電流値	太さ	許容電流値
1.6[mm]	27[A]	2[mm2]	27[A]
2.0[mm]	35[A]	3.5[mm2]	37[A]
2.6[mm]	48[A]	5.5[mm2]	49[A]
3.2[mm]	62[A]	8[mm2]	61[A]
		14[mm2]	88[A]

問題より直径1.6mmの電線を3本収めて施設する。とあるので直径1.6mmの電線の許容電流値は27Aです。
電流減少係数が0.70なので
27 x 0.7=18.9

【答え・イ】

Sponsored link