電気入門
総合情報.com

電気の基礎入門及び電気工事士資格対策サイトです。

令和4年度上期午後

問題1

図のような回路で，スイッチ S を閉じたとき， a b端子間の電圧［V］は。



• イ.30
• ロ.40
• ハ.50
• ニ.60

---

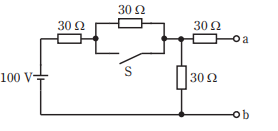
【解説】

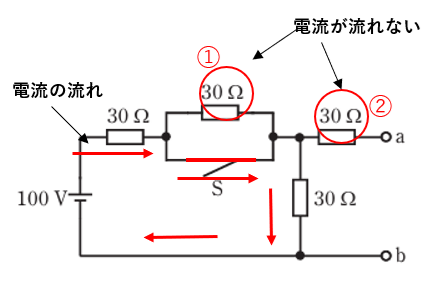
スイッチSを閉じたら①には電流が流れません。
また②にはそもそもaとbが閉じられていないので電流は流れません。
従ってスイッチSを閉じたら以下のようになります。

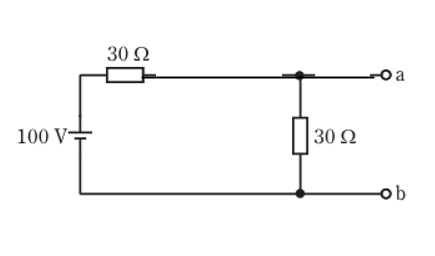
電圧は、「100V」で、30Ωを2つに分圧しているので
50Vになります。

【答え・ハ】

問題3

電線の接続不良により，接続点の接触抵抗が0.2Ω となった。この接続点での電圧降下が 2 Vのとき，接続点から 1 時間に発生する熱量［kJ］は。
ただし，接触抵抗及び電圧降下の値は変化しないものとする。
• イ.72
• ロ.144
• ハ.288
• ニ.576

---

【解説】

この問題は以下の公式を使います。

• V=IR
• P=I²R
• H=P x t

まずオームの法則より電流を求めます。
問題より抵抗が0.2Ω、電圧が2Vなので
V=IR
より
2 = I x 0.2
I=10A
次に電力の公式
P=IV=I x I x R=I²R
より
P=10 x 10 x 0.2=20W
次に熱量の公式より
H = P x t
ここで時間が1時間とありますが1時間を秒に変換しなければいけません。
1分=60秒　x 60分＝3600秒
H=20 x 3600=72000W=72[KJ]

【答え・イ】

問題4

コイルに 100 V，50 Hz の交流電圧を加えたら 6 A の電流が流れた。このコイルに 100 V，60 Hz の交流電圧を加えたときに流れる電流［A］は。
ただし，コイルの抵抗は無視できるものとする
• イ.4
• ロ.5
• ハ.6
• ニ.7

---

【解説】

結構難しい問題と思います。
まずコイルに流れる電流は以下の公式で求めることができます。

ここで問題より100 V，50 Hz の交流電圧を100 V，60 Hz の交流電圧に代えた場合の電流を答えなさいとなっています。
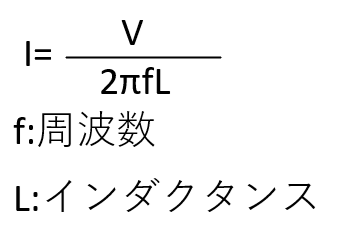
上記公式より
電圧VとインダクタンスLが変わらない場合、電流は、周波数fと反比例することがわかります。
従って

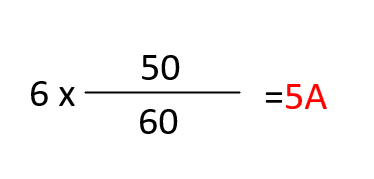
【答え・ロ】

問題5

図のような三相 3 線式回路の全消費電力［kW］は。



• イ.2.4
• ロ.4.8
• ハ.9.6
• ニ.19

---

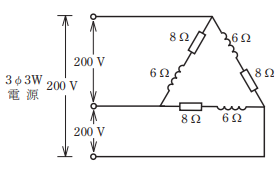
【解説】

1相分のインピーダンスZは

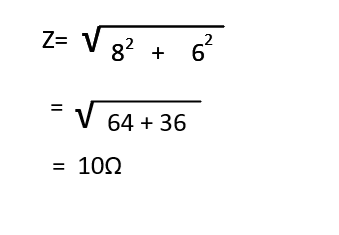
Z=10Aから、相電流を求めると 200 = I x 10
I=20A
になります。
P=I²R
より
P=20 x 20 x 8 = 3200W
これは1相分なので3相分の消費電力を求めるために3倍します。
3 x 3200=9600=9.6[kW]
消費電力を求めているので抵抗負荷のみで計算しなければなりません。

【答え・ハ】

問題6

図のように，単相 2 線式電線路で，抵抗負荷A，B，C にそれぞれ負荷電流 10 A が流れている。電源電圧が 210 V であるとき抵抗負荷 C の両端電圧 V_C［V］は。
ただし，r は電線の抵抗［Ω ］とする。



• イ.198
• ロ.200
• ハ.202
• ニ.204

---

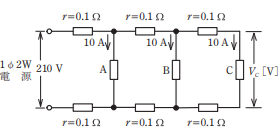
【解説】

単相2線式の電圧降下を求めるには以下の公式を使います。

• 2rI

まずもって、右端の「B-C」間から見ていきます。 問題文の図より、rは0.1Ωで、Iは10Aなことがわかります。
2rIの公式に当てはめると
V=2 x 0.1 x 10 = 2V
次に真ん中の「A-B」間を見ていきます。
問題文の図より、rは0.1Ωです。
ここで注意ですがIは10 + 10 = 20Aです。
V=2 x 0.1 x 20 = 4V
次に、左側のA間を見ていきます。
問題文の図より、rは0.1Ωです。

ここで注意ですがIは10 + 10 + 10 = 30Aです。
V=2 x 0.1 x 30 = 6V
従ってこれらが電圧降下したことになります。
2 + 4 + 6 = 12V
電圧降下しています。
もともとの電源電圧が210Vなので
210 - 12 =198V
になります。

【答え・イ】

問題7

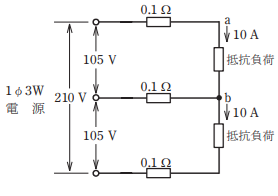
図のような単相 3 線式回路において，電線 1線当たりの抵抗が 0.1Ωのとき， a b間の電圧［V］は。



• イ.102
• ロ.103
• ハ.104
• ニ.105

---

【解説】

この問題は単相3線式回路の電圧降下の問題です。
しかもab間の電圧降下を求めてやります。

• 単相2線式・・・2Ir
• 単相3線式・・・Ir

より
問題の図から、ｒは0.1Ωで、Ｉは10Aであることがわかります。
0.1 x 10 = 1V
問題の図よりab間の電源電圧が105Vなので
105-1=104V
になります。

【答え・】

問題8

金属管による低圧屋内配線工事で，管内に直径2.0 mm の 600V ビニル絶縁電線(軟銅線)2 本を収めて施設した場合，電線 1 本当たりの許容電流［A］は。ただし，周囲温度は 30 ℃以下，電流減少係数は 0.70 とする。
• イ.19
• ロ.24
• ハ.27
• ニ.35

---

【解説】

この問題は以下のことを覚えておかなければなりません。

単線		より線
太さ	許容電流値	太さ	許容電流値
1.6[mm]	27[A]	2[mm2]	27[A]
2.0[mm]	35[A]	3.5[mm2]	37[A]
2.6[mm]	48[A]	5.5[mm2]	49[A]
3.2[mm]	62[A]	8[mm2]	61[A]
		14[mm2]	88[A]

問題では直径2.0mmの電線を2本収めて施設する。とあるので
直径2.0mmの単線の許容電流は35Aになります。
問題より電流減少係数は 0.70とあるので
35 x 0.7=24.5

【答え・ロ】

問題9

図のように，三相の電動機と電熱器が低圧屋内幹線に接続されている場合，幹線の太さを決める根拠となる電流の最小値［A］は。
ただし，需要率は 100％とする。
• イ.70
• ロ.74
• ハ.80
• ニ.150

---

【解説】

この問題は以下のことを覚えておかなければいけません。

幹線に求められる許容電流

幹線の許容電流(電流の太さ)は、負荷の定格電流の場合よって決まります。
特に負荷に電動機は始動するときに大きな電流が流れるため、余裕をもって許容電流を決めなければいけません。

電動機の定格電流が小さい場合

電動機の定格電流の総量IMが、その他の負荷の定格電流の総量IHより小さいか等しい場合は以下のように幹線の許容電流は決まります。

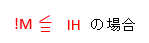
幹線の許容電流はIWは

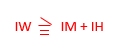
になります。

電動機の定格電流が大きい場合

電動機の定格電流の総量IMが、その他の負荷の定格電流の総量IBより大きい場合は、以下のように幹線の許容電流は決まります。

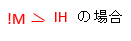
幹線の許容電流はIWは

になります。

電動機の定格電流IMを計算します。
問題より
電動機Mは定格電流10Aと定格電流30Aが2台あります。
IM=10 + 30=40A
需要率は100%なので、40のままです。
ここで需要率が85%とかなっていたら
40 x 0.85=34
のようにしなければいけませんが今回は100%なのでそのままでいいです。
次に電熱機の定格電流IHを計算します。
電熱器は定格電流15Aと定格電流15Aが2台あります。
IH=15 + 15=30
になります。
ここでも需要率が100%なのでそのまま30Aになります。
従って
IM=40A
IH=30A
IM=40なので
50A以下であるため、「IM ≦ 50A」のところに該当します。
公式より
IW ≧ 1.25IM+IH
IW ≧ 1.25 x 40+30
IW ≧ 50+30
IW ≧ 80

【答え・ハ】

Sponsored link