令和4年度上期午前
問題1
-
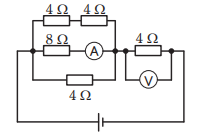
図のような回路で,電流計 Aの値が 1 A を示した。このときの電圧計 Vの指示値[V]は。
- イ.16
- ロ.32
- ハ.40
- ニ.48
【解説】
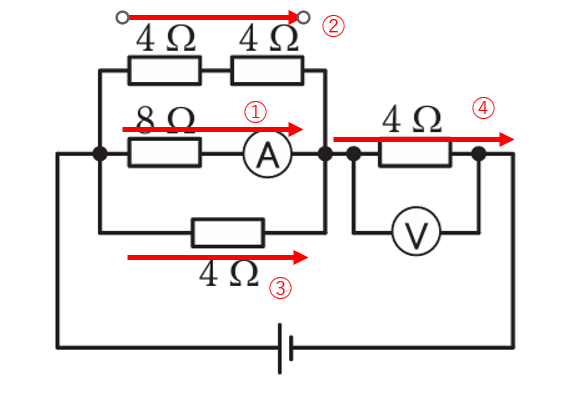
①真ん中の「8Ω」のところの「電圧」を求めます。
問題文から電流計 Aの値が 1 A を示した。
とありますので
オームの法則
V=IR
より
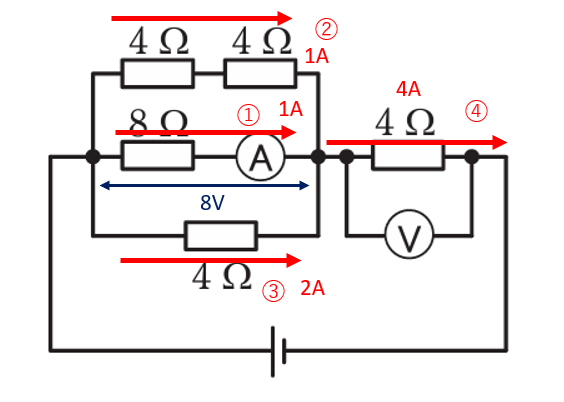
V=1 x 8 = 8V
になります。
②次に4Ωと4Ωに流れている電流を求めます。
4Ωと4Ωは直列接続なので合成抵抗は
4 + 4=8Ω
になります。
①で電圧が8Vと分かったので
V=IR
より
8=I x 8より
I = 1A
になります。
③次に4Ωに流れている電流を求めます。
V=IR
より
8=I x 4より
I = 2A
になります。
④に流れている電流は
①+②+③=④なので
1+1+2=4A
電圧計 Vの指示値[V]は
V=IR
より
4 x 4=16V
になります。
【答え・イ】
問題3
- 抵抗器に100 Vの電圧を印加したとき,5 Aの電流が流れた。1時間30分の間に抵抗器で発生する熱量[kJ]は。
- イ.750
- ロ.1800
- ハ.2700
- ニ.5400
【解説】
熱量計算Hの公式は、H[J]=P[W] x tです。
Pは、P=IV
で求めることができます。
tは時間のことです。
ここで注意があります。
ここでの時間は「秒」です。
従って問題文の1時間30分を秒の単位に変換しなけれいけません。
したがって
1時間30分=90分
1分=60秒
90分=90 x 60 = 5400秒
になります。
Pを求めると
P= 100 x 5=500W
です。
従って熱量は
熱量計算Hの公式は、H[J]=P[W] x t
より
500 x 5400=2700000J=2700[kJ]
になります。
【答え・ハ】
問題4
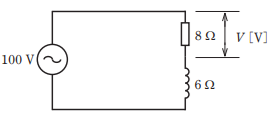
- 図のような交流回路において,抵抗 8Ω の両端の電圧 V[V]は。
- イ.43
- ロ.57
- ハ.60
- ニ.80
【解説】
少し難しい問題になります。
当該回路のインピーダンスを求めます。
8Ωの抵抗と6Ωのコイルのインピータンスは以下のようになります。
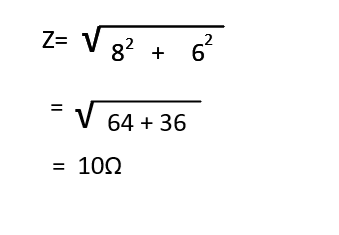
V=Ix Z
で求めることができます。
V = I x 10
より
I=10A
になります。
従って抵抗 8Ω の両端の電圧 V[V]は
V=IR
より
V=10 x 8 =80V
になります。
【答え・ニ】
問題5
- 図のような三相3線式回路の全消費電力[kW]は。
- イ.2.4
- ロ.4.8
- ハ.7.2
- ニ.9.6
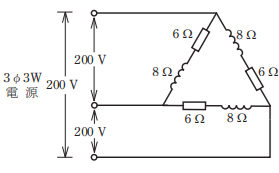
【解説】
1相分のインピーダンスZは
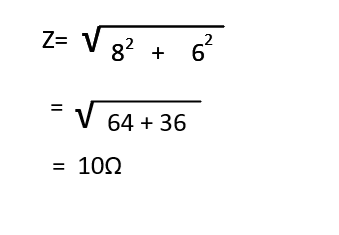
次に相電流を求めます。
Z=10Ω
より
相電流を求めると
V=IZ
より
200 = I x 10
I = 20A
P=I x V
=I x I x R = 20 x 20 x 6 = 2400W
ここで消費電力を求めるので抵抗のみで計算します。
最後に2400Wは1相分の消費電力なので3相分で計算します。
3 x 2400 = 7200W=7.2[kW]
【答え・ハ】
問題6
-
図のような三相 3 線式回路で,電線 1 線当たりの抵抗が0.15Ω ,線電流が10 Aのとき,この電線路の電力損失[W]は。
- イ.15
- ロ.26
- ハ.30
- ニ.45
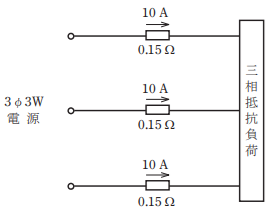
【解説】
三相3線式回路の電力損失を問う問題です。
電力損失の公式で求めることができますので公式は暗記しておきましょう。
- 単相2線式・・・・2rI2
- 単相3線式・・・・2rI2
- 三相3線式・・・・3rI2
3 x 0.15 x 10 x 10 = 45W
今回は電流が線電流なので3を掛けましたが相電流の場合は少し異なるので気を付けましょう。
【答え・ニ】
問題7
-
図のような単相 3 線式回路において,消費電力 1 000 W,200 W の 2 つの負荷はともに抵抗負荷である。図中のX印点で断線した場合, a - b 間の電圧[V]は。
- イ.17
- ロ.33
- ハ.100
- ニ.167
ただし,断線によって負荷の抵抗値は変化しないものとする
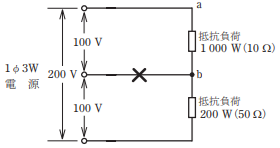
【解説】
単相3線式回路にて、真ん中の中性線が断線すると、両抵抗には、200Vの電圧がかかります。
従って
回路に流れる電流は
V=IR
より
200 = I x (10 + 50 )
I=3.33
になります。
今回の問題は
a - b 間の電圧なので
V=IR
より
V=3.3 x 10=33[V]
になります。
【答え・ロ】
問題8
-
金属管による低圧屋内配線工事で,管内に直径 2.0 mm の 600V ビニル絶縁電線(軟銅線)4 本を収めて施設した場合,電線 1 本当たりの許容電流[A]は。
- イ.22
- ロ.31
- ハ.35
- ニ.38
ただし, 周囲温度は 30 ℃以下, 電流減少係数は 0.63 とする。
【解説】
この問題は以下のことを覚えておかなければなりません。
| 単線 | より線 | ||
|---|---|---|---|
| 太さ | 許容電流値 | 太さ | 許容電流値 |
| 1.6[mm] | 27[A] | 2[mm2] | 27[A] |
| 2.0[mm] | 35[A] | 3.5[mm2] | 37[A] |
| 2.6[mm] | 48[A] | 5.5[mm2] | 49[A] |
| 3.2[mm] | 62[A] | 8[mm2] | 61[A] |
| 14[mm2] | 88[A] | ||
直径「2.0mm」の電線を「4本」収めて施設する、とあります。
つまり
2.0mmの許容電流は上の表より35Aとあります。
また、 電流減少係数は 0.63とあるので
35 x 0.63 = 22.05
【答え・イ】
問題9
-
定格電流 12 A の電動機 5 台が接続された単相 2 線式の低圧屋内幹線がある。この幹線の太さを決定するための根拠となる電流の最小値[A]は。
- イ.48
- ロ.60
- ハ.66
- ニ.75
ただし,需要率は 80%とする。
【解説】
この問題は以下のことを覚えておかなければいけません。
幹線に求められる許容電流
幹線の許容電流(電流の太さ)は、負荷の定格電流の場合よって決まります。
特に負荷に電動機は始動するときに大きな電流が流れるため、余裕をもって許容電流を決めなければいけません。
電動機の定格電流が小さい場合
電動機の定格電流の総量IMが、その他の負荷の定格電流の総量IHより小さいか等しい場合は以下のように幹線の許容電流は決まります。
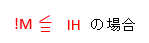
幹線の許容電流はIWは
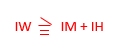
になります。
電動機の定格電流が大きい場合
電動機の定格電流の総量IMが、その他の負荷の定格電流の総量IBより大きい場合は、以下のように幹線の許容電流は決まります。
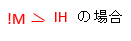
幹線の許容電流はIWは

になります。
最初に、電動機(M)の「IM」から求めます。問題文より、定格電流 12 A の電動機 5 台が接続とあるので
15 x 5 =60A
になります。
ここで、需要率が80%なので
60 x 80%(0.8)=48A
になります。
この問題では電動機のみで、電熱器がありません。
従って
Im > IH
になります。
IM ≦ 50Aに該当します。
公式から、「IW ≧ 1.25IM+IH」に該当します。
IW ≧ 1.25IM + IH
IW ≧ 1.25 x 48 + 0
IW ≧ 60
【答え・ロ】
Sponsored link





