電気入門
総合情報.com

電気の基礎入門及び電気工事士資格対策サイトです。

令和3年度上期午後

問題1

図のような回路で、8Ωの抵抗での消費電力[W]は。



• イ.200
• ロ.800
• ハ.1200
• ニ.2000

---

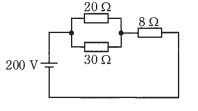
【解説】

8Ωの抵抗の消費電力[W]は以下の式で求めることができます。

つまり
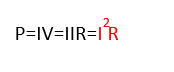
8Ωに流れる電流が分かれば消費電力が分かります。
8Ωに流れる電流Iは

になりますので
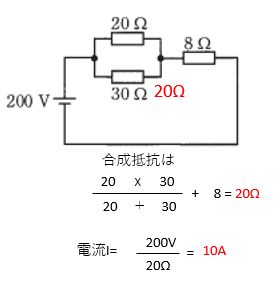
消費電力P=I² x 8=800W
従ってロになります。

【答え・ロ】

問題2

直径2.6mm長さ20mの銅導線と抵抗値が最も近い同材質の銅導線は。
• イ.断面積8mm²、長さ40m
• ロ.断面積8mm²、長さ20m
• ハ.断面積5.5mm²、長さ40m
• ニ.断面積5.5mm²、長さ20m

---

【解説】

まず

• 導線の抵抗値は、導線の長さに比例します。つまり、長さが2倍、3倍となれば、抵抗値も2倍、3倍になります。
• 導線の抵抗値は、導線の断面積に反比例します。つまり、断面積が2倍、3倍となれば、抵抗値は1/2倍、1/3倍になります。

問題文では、導線の断面積ではなく、直径で条件が与えられている部分があります。抵抗値は、断面積がわかっているほうが比較しやすいので、直径から断面積を計算します。
断面積=半径　x　半径　x　円周率
になります。
半径は直径÷2
円周率は3.14
で計算すると
断面積=1.3 x 1.3 x 3.14=5.3mm²
になります。
従って問題文は
断面積5.3mm²長さ20mの銅導線と抵抗値が最も近い同材質の銅導線は。
に書き換えることは出来ました。
上記で述べた長さが倍なら抵抗値も倍になり（比例する）、断面積が倍なら抵抗値は半分になる（反比例する）

• イは断面積1.51倍で長さが2倍なので2÷1.51=抵抗が1.32倍
• ロは断面積1.51倍で長さが1倍なので1÷1.51=抵抗が0.66倍
• ハは断面積1.03倍で長さが2倍なので2÷1.03=抵抗が1.94倍
• ニは断面積1.03倍で長さが1倍なので1÷1.03=抵抗が0.97倍

になり抵抗値が最も近い(1に近いのは)ニになります。

【答え・ニ】

問題3

消費電力が400Wの電熱器を1時間20分使用した時の発熱量[kJ]は。
• イ.960
• ロ.1920
• ハ.2400
• ニ.2700

---

【解説】

発熱量＝（消費電力）W×秒数
になります。
今回は1時間20分なので
1時間20分=80(分) x 60 =4800秒
400 x 4800=1920000=1920[kJ]
になります。

【答え・ロ】

問題4

図のような回路で、電源電圧が24V、抵抗R=4Ωに流れる電流が6A、リアクタンスXL=3Ωに流れる電流が8Aであるとき、回路の力率「%]は。



• イ.43
• ロ.60
• ハ.75
• ニ.80

---

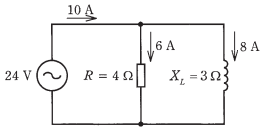
【解説】

力率は抵抗のみについて考えればいいので、回路の電流がI
抵抗に流れる電流がI_Rとすると以下の式で求めることができます。

【答え・ロ】

問題5

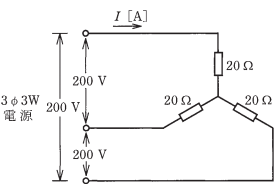
図のような三相3線式回路に流れる電流I[A]は。



• イ.2.9
• ロ.5.0
• ハ.5.8
• ニ.10.0

---

【解説】

この回路はスター(Y)回路になるので
相電流=線間電流
になります。
つまり以下の図のようになります。

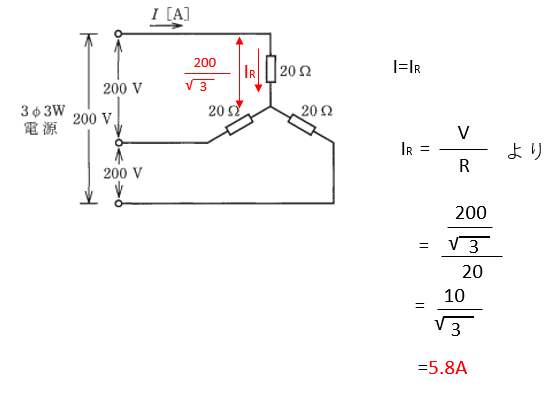
【答え・ハ】

Sponsored link