令和元年度下期
問題1
- 図のような回路で、端子a-b間の合成抵抗[Ω]は。
- イ.1
- ロ.2/li>
- ハ.3
- ニ.4
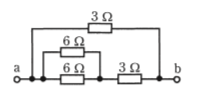
【解説】
合成抵抗は以下の順に合成抵抗を求めていきます。
①の6Ωと6Ωの並列回路
②の直列回路
③の並列回路
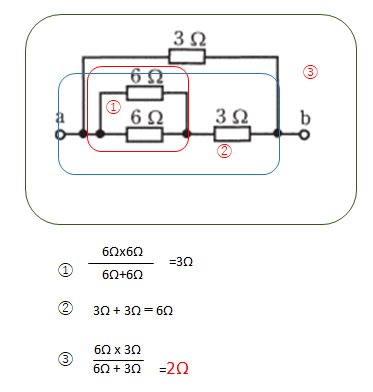
【答え・ロ】
問題2
- 直径2.6mm、長さ10mの銅導線と抵抗値が最も近い同材質の銅導体は。
- イ.断面積5.5mm2、長さ10m
- ロ.断面積8mm2、長さ10m
- ハ.直径1.6mm 長さ20m
- ニ.直径3.2mm、長さ5m
【解説】
- 導線の抵抗値は、導線の長さに比例します。つまり、長さが2倍、3倍となれば、抵抗値も2倍、3倍になります。
- 導線の抵抗値は、導線の断面積に反比例します。つまり、断面積が2倍、3倍となれば、抵抗値は1/2倍、1/3倍になります。
問題文では、導線の断面積ではなく、直径で条件が与えられている部分があります。
抵抗値は、断面積がわかっているほうが比較しやすいので、直径から断面積を計算します。
断面積=半径 x 半径 x 円周率
になります。
半径は直径÷2
円周率は3.14
で計算すると
問題で直径2.6mmの断面積を求めると
断面積=1.3 x 1.3 x 3.14=5.3mm2 になります。
従って問題文は
断面積5.3mm2長さ10mの銅導線と抵抗値が最も近い同材質の銅導線は。
と同じことになります。
ハの1.6mmの断面積は
0.8 x 0.8 x 3.14=2.0mm2
ニの3.2mmの断面積は
1.6 x 1.6 x 3.14=8mm2 断面積が最も近くて長さが同じイが正しい。
【答え・イ】
問題3
- 消費電力が500Wの電熱器を、1時間30分使用したときの発熱量[kJ]は。
- イ.450
- ロ.750
- ハ.1800
- ニ.2700
【解説】
発熱量=(消費電力)W×秒数
になります。
今回は1時間30分なので
1時間30分=1.5 x 60 x 60 =5400秒
になり
500 x 5400=2700000=2700[kJ]
になります。
【答え・ニ】
問題4
- 図のような正弦波交流回路の電源電圧vに対する電流iの波形として、正しいものは。
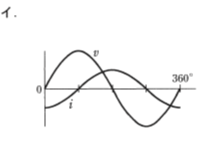
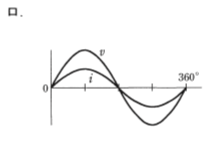
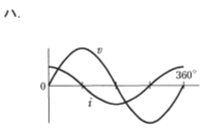
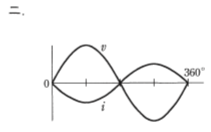
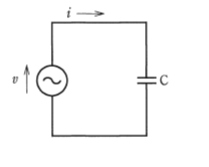
【解説】
正弦波交流電源に静電容量(コンデンサ)Cが接続されると、電流iの波形は電圧vの波形より90℃位相が進む。
逆に、正弦波交流電源にインダクタンス(コイル)Lが接続されると、電流iの波形は電圧vの波形より位相が遅れる。
従ってハが正しい。
【答え・ハ】
問題5
- 図のような三相3線式回路に流される電流I[A]は。
- イ.8.3
- ロ.12.1
- ハ.14.3
- ニ.20.0
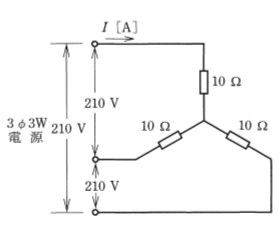
【解説】
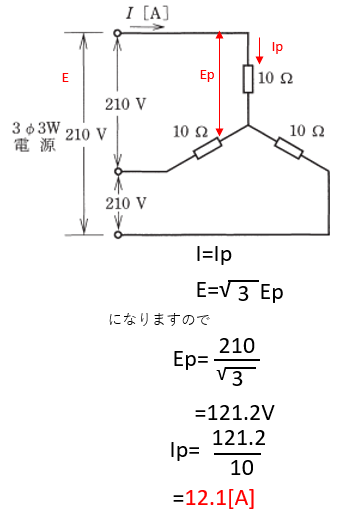
従ってロになります。
【答え・ロ】
Sponsored link





