電気入門
総合情報.com

電気の基礎入門及び電気工事士資格対策サイトです。

令和7年下期

問題1

図のような平行平板キャパシタにおいて，電極間に 100 V の電圧を加えたとき，電極間に何も挟んでいない（空気）キャパシタ内の電界の強さ E［V/m］は。
ただし，電極間の距離 d=1 x 10^-3m，平行平板間の電界は平等電界とする。



• イ.1 x 10²
• ロ.1 x 10³
• ハ.1 x 10⁴
• ニ.1 x 10⁵

---

【解説】

この問題を解くには以下の公式は必ず覚えておく必要があります。

• 電界の強さ(E=V/d[V/m])
• 静電容量(C=εA/d[F ファラッド])
• 電荷量(CV[c クーロン)])
• 蓄えられたエネルギー(W=1/2 x CV²[J ジュール)])

※εは誘電率です。

今回の問題では
電界の強さ(E=V/d[V/m])を用いて求めす。
問題より
電極間の電圧Vが100V
電極間の距離Dは1 x 10^-3m
とあるので
公式に代入するだけです。
E=V/d[V/m]より
E=100 / 1 x 10^-3
=1 x 10⁵
になりますので二が正解です。

【答え・二】

問題2

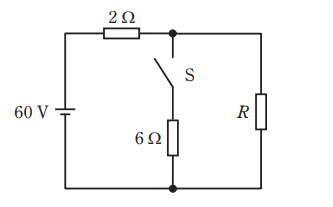
図のような直流回路において，スイッチ Sが開いているとき，抵抗 R の両端の電圧は36 V であった。スイッチ S を閉じたときの抵抗 R の両端の電圧[V]は。



• イ.3
• ロ.12
• ハ.24
• ニ.30

---

【解説】

まず抵抗Rの両端の電圧は36Vであるので
電源電圧が60Vより
2Ωの所の電圧は
60-36=24V
になり
I= 24/2=12A
になります。
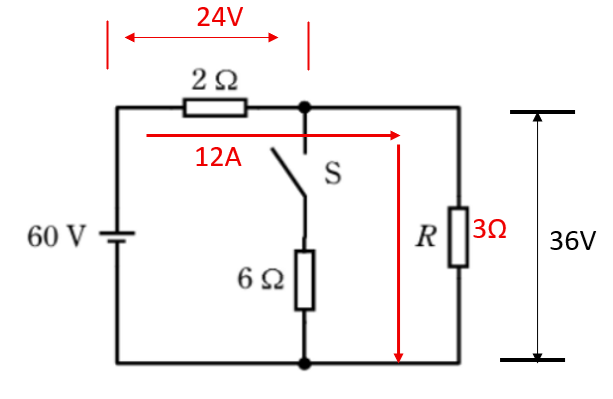
またRですがRにも12A流れているので
R=36/12=3Ω
になります。

次にスイッチを閉じたときの回路は以下のようになります。

6Ωと3Ωは並列接続になっているので合成抵抗は和分の積を使って求めると

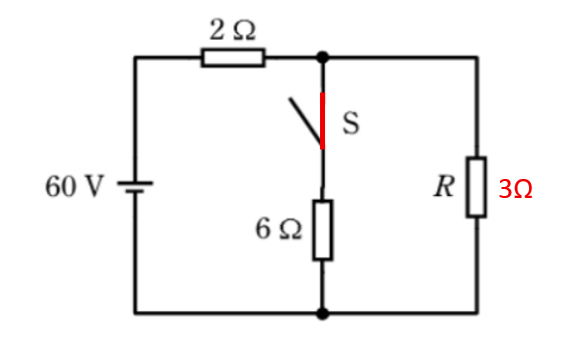
6Ω x 3Ω / 6Ω + 3Ω=18 / 9 = 2Ω
になります。

このようになり
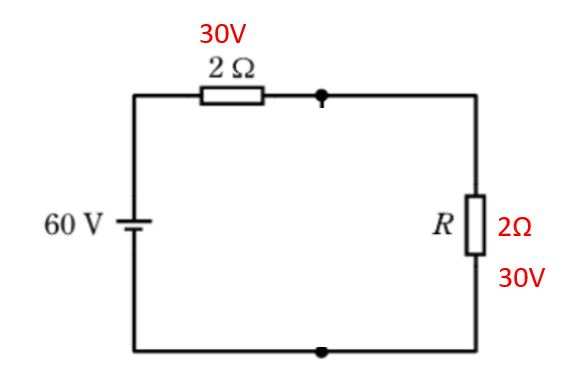
合成抵抗の両端の電圧は60Vを2Ωと2Ωに分圧するので30Vになります。

【答え・二】

問題3

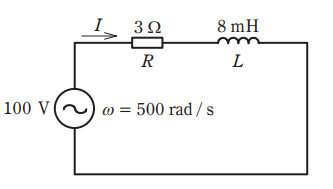
図のように，角周波数がω = 500 rad/s，電圧100 V の交流電源に，抵抗 R= 3Ω とインダクタンス L= 8 mH が接続されている。回路に流れる電流 I の値[A]は。



• イ.9
• ロ.14
• ハ.20
• ニ.33

---

【解説】

以下の公式を使います。

つまり XL=500 x 8 x 10^-3=4Ω
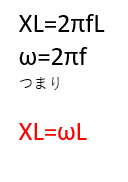
になります。
回路のインピータンスZ(Ω)は

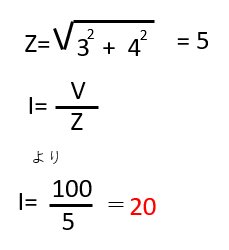
【答え・ハ】

問題4

図のような交流回路において，10Ω の抵抗の消費電力[W]は。
ただし，ダイオードの電圧降下や電力損失は無視する。



• イ.100
• ロ.200
• ハ.500
• ニ.1000

---

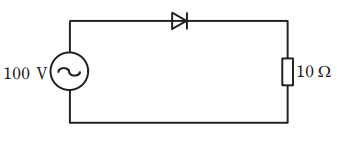
【解説】

この図の回路では
P=E² / R
で
P = 100 x 100 / 10 = 10000 / 10 = 1000W
になります。
今回の問題ではダイオードがあります。
ダイオードの場合は半波整流されるので、交流電力は半分になります。
したがって
1000Wの半分の500Wになります。

【答え・ハ】

問題5

図のような三相交流回路において，電源電圧は V[V]，抵抗 R= 5Ω ，誘導性リアクタンス XL= 3Ω である。回路の全消費電力[W]を示す式は。



• イ.3V² / 5
• ロ.V²/ 3
• ハ.V² / 5
• ニ. V²

---

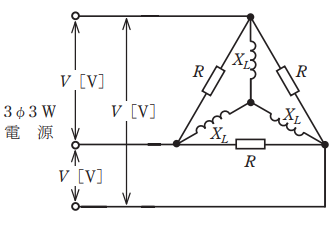
【解説】

今回のポイントは求めるのが回路の全消費電力[W]です。
消費電力ということは有効電力になりますのでコイルXLは無視できます。
消費電力の公式
P=IV
でした。
まず1相分の消費電力を求めると
今回は抵抗成分を式にいれないといけないので
V=IR
より
I=V/R
P=(V/R) x V
V²/R
になります。
R=5Ω
ですので
1相分の消費電力Pは
P=V² / 5
になります。
3相分は3倍しますので
3 x V² / 5
しないといけません。
全消費電力Pは
P=3V² / 5
になります。

【答え・イ】

Sponsored link