令和7年度上期
問題1
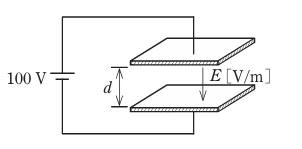
- 図のような平行平板キャパシタにおいて,電極間に100 Vの電圧を加えたとき,電極間に何も挟んでいない(空気)キャパシタ内の電界の強さE[V/m]は。
- イ.1×102
- ロ.1×103
- ハ.1×104
- ニ.1×105
ただし,電極間の距離d=1× 10-3m,平行 平板間の電界は平等電界とする。
【解説】
電界の強さE=V ÷ m
なので
E=100 ÷ 1 x 10-3=1×105[V/m]
になります。
したがって二が正しいです。
【答え・ニ】
問題2
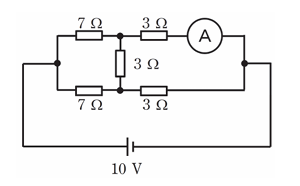
- 図のような直流回路において,電流計に流れる電流[A]は。
- イ.0.1
- ロ.0.5
- ハ.1.0
- ニ.2.0
【解説】
この回路は対角線上の抵抗〇7Ωと3Ωと□7Ωと3Ωなのでブリッジ回路の平衡しています。
この場合は真ん中の3Ωには電流が流れません。
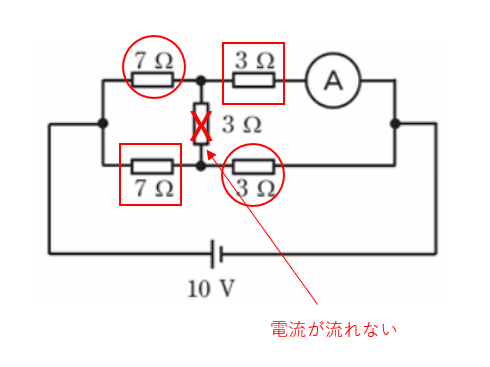
7Ω+3Ω=10Ω
の並列回路になります。
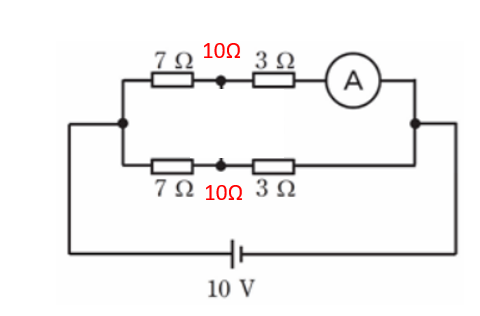
R=10 x 10 / 10 + 10 =5Ω
になります。
この回路に流れる電流Iは
V=IR
I=V/R=10/5=2[A]
になります。
上の回路にも10Ω下の回路のも同じ10Ωの抵抗がありますので
2Aのうち1Aずつ流れていることになります。
したがって答えはハの1.0[A]です。
【答え・ハ】
問題3
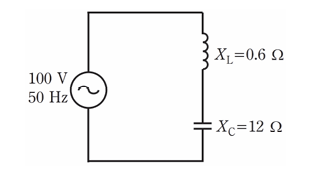
- 図のような交流回路において,電源が電圧100 V,周波数が50 Hzのとき,誘導性リアクタンスXL= 0.6Ω ,容量性リアクタンスXC= 12Ω である。この回路の電源を電圧100 V, 周波数60 Hzに変更した場合,回路のインピーダンス[Ω]の値は。
- イ.9.28
- ロ.11.7
- ハ.16.9
- ニ.19.9
【解説】
各リアクタンスは、周波数f[Hz]、インダクタンスL[H]、静電容量を用いると以下の公式になります。
XL=2πfL、Xc=1/2πfC
したがってXLは周波数に比例し、XCは周波数に反比例します。
つまりXLの場合は50Hzから60Hzにした場合は大きく
XCの場合は50Hzから60Hzにした場合は小さくなります。
実際計算していくと
XL=60/50 x 0.6=0.72Ω
XC=50/60 x 12=10Ω
になります。
今回はこの回路のインピーダンス[Ω]を求めて行くので
10-0.72=0.98Ω
になります。
【答え・イ】
問題4
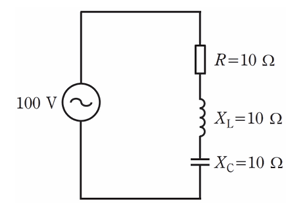
- 図のような交流回路において,抵抗R=10Ω , 誘導性リアクタンスXL=10Ω ,容量性リアク タンスXC =10Ω である。この回路の力率[%]は。
- イ.30
- ロ.50
- ハ.70
- ニ.100
【解説】
この問題はXL=10ΩでXC=10Ωなのでこの部分は打ち消しあって0Ωになりますので
実際抵抗のみの回路となります。
抵抗しかない回路の力率は100%です。
したがって二が正しい。
【答え・ニ】
問題5
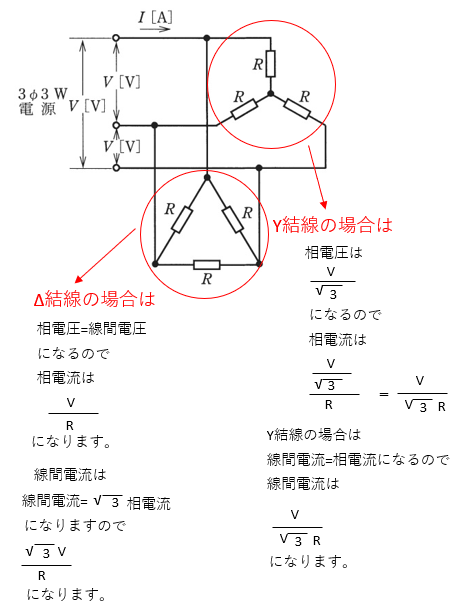
図のように,線間電圧V [V]の三相交流電源から,Y結線の抵抗負荷とΔ結線の抵抗負荷に電力を供給している電路がある。図中の抵抗RがすべてR [Ω]であるとき,図中の電路の線電流I [A]を示す式は。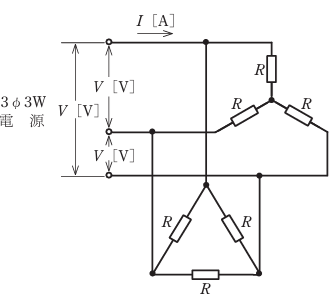
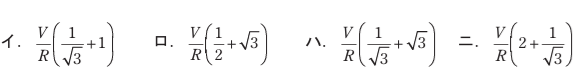
【解説】
この問題はY結線の負荷に接続している電線に流れる電流IYとΔ結線の負荷に接続している電線に流れる電流IΔを求めて
その和を求めていきます。
つまり
IY + IΔ
になります。
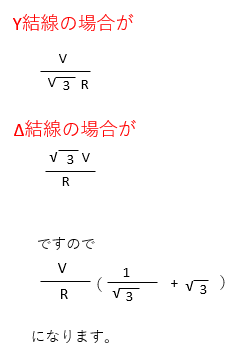
【答え・ハ】
Sponsored link





