電気入門
総合情報.com

電気の基礎入門及び電気工事士資格対策サイトです。

令和6年度上期

問題1

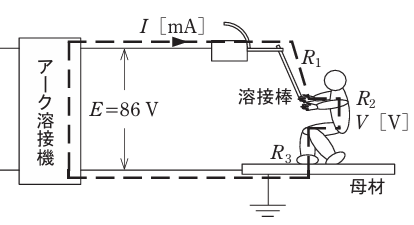
図のようなアーク溶接作業での感電において、人体を通って流れる電流I[mA]と人体抵抗R2にかかる電圧V[V]は。
ただし、溶接機の出力側無負荷電圧E=86V、乾燥した状態の保護手袋や作業靴を着用しているとき、手と溶接棒間の抵抗R₁=20kΩ、人体の抵抗R₂=500Ω、足と母材間の抵抗R₃=30kΩとする。



• イ. I=1.7
  V=42
• ロ.I=17
  V=42
• ハ.I=1.7
  V=0.85
• ニ. I=17
  V=0.85

---

【解説】

答えはハになります。
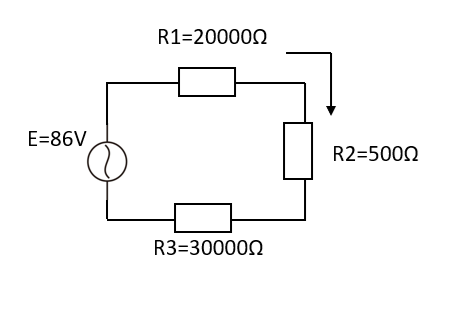
わかりやすく書き換えると以下のようになります。

流れる電流はオームの法則より
E=IR
I=E/R
で求めることができます。抵抗はR1とR2とR3が直列接続になっているのでそのまま足すことができます。
R1+R2+R3=20000+500+30000=50500Ω
になります。
電圧は86Vなので
I=86 / 50500=0.0017[A]=1.7[mA]
になります。
人体にかかる電圧は
E(人体にかかる電圧)=R2 x I
で求めることができるので
E=500 x 0.0017= 0.85[V]
になります。

【答え・ハ】

問題2

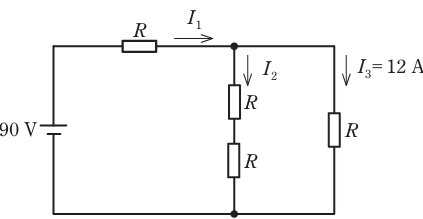
図のような直流回路において、4つの抵抗Rは同じ抵抗値である。回路の電流I₃が12Aであるとき、抵抗Rの抵抗値[Ω]は。



• イ.2
• ロ.3
• ハ.4
• ニ.5

---

【解説】

ポイントとしては4つの抵抗が同じ抵抗値ということです。
つまり
I₂のところにはRが直列に2つありますので2Rとなります。
またI₃=12A
になりますので
2R x I₂=R x 12[A]
より
I₂=6[A]
I₁=I₂+I₃=18[A]
になります。
ここで電圧が90Vで回路に流れる電流が18Aなので回路の合成抵抗は
E=IR
R=E/I=90 / 18=5[Ω]
になります。 次に

とすると
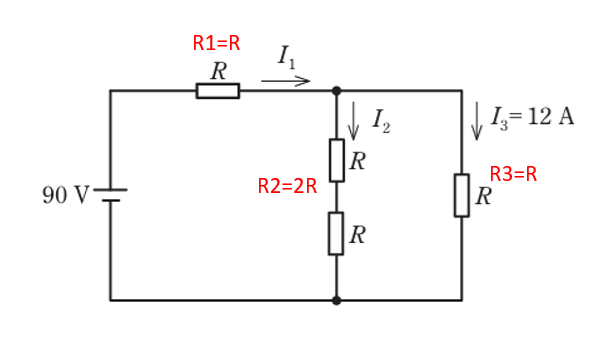
R2とR3は並列なので和分の積で求めます。
それにR1が直列になっているので以下のようになります。 合成抵抗RはR1 + R2 x R3 /R2 + R3
になります。
R=R + 2R x R / 2R + R = R + 2/3R=5/3R
になります。
つまり
R=5[Ω]なので
5 = 5/3R
R=5 x 3/5=3[Ω]
になります。

【答え・ロ】

問題3

図のような交流回路において、電源電圧は100V、電流は20A、抵抗Rの両端の電圧は80Vであった。リアクタンスX[Ω]の値は。



• イ.2
• ロ.3
• ハ.4
• ニ.5

---

【解説】

まず電源電圧100Vと電流からインピータンスZが求められます。
オームの法則より
E=IZ
Z=E/I=100 / 20 = 5[Ω]になります。
次にRにかかる電圧が80VでRに流れる電流が20Aですので
これもオームの法則で
E=IR
R=E/R=80 / 20 = 4[Ω]
になります。 あとはピタゴラスの定理を利用してリアクタンスを求めます。

になりますので
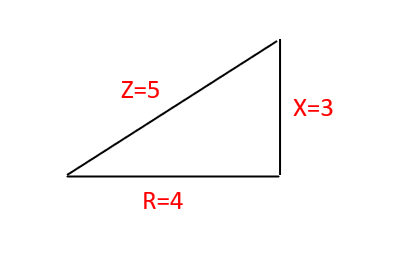
リアクタンスXは3Ωになります。

【答え・ロ】

問題4

定格電圧100V、定格消費電力1kWの電熱器の電熱線が全長の10%のところで断線したので、その部分を除き、残りの90%の部分を電圧100Vで1時間使用した場合、発生する熱量[kJ]は。
ただし、電熱線の温度による抵抗の変化は無視するものとする。
• イ.2900
• ロ.3600
• ハ.4000
• ニ.4400

---

【解説】

まずは断線する前の電流を求めます。
定格消費電力1kW、定格電圧100Vなので
P=IV
I=P/V=1000 / 100 = 10[A]
次に断線する前の抵抗を求めると
V=IR
R=V / I=100 / 10 = 10[Ω]
になります。 そこでポイントは
電熱線が全長の10%のところで断線したので、その部分を除き、残りの90%の部分
とあります。
つまり断線する前の抵抗が1倍とすると断線後の抵抗は0.9倍になります。
抵抗が小さくなるともちろん電流は増えて1/0.9倍になります。

次に断線後の電流を求めると
1/0.9倍なので
断線前の電流が10Aなので
10 x 1/0.9=11.1A
断線後の抵抗を求めると
断線前の抵抗が10Ωなので
10 x 0.9 = 9Ω
になります。
断線後の電力を求めると
P=I²R
で求めることができるので
P=11.1²x9=1108.89W
になります。
最後に断線後の電力量を求めていきます。
W=Pt
より
W=1108.89 x 3600=3992000W
になりますので
およそ4000[kJ]
になります。

【答え・ハ】

問題5

図のような三相交流回路において、電源電圧は200V、抵抗は4Ω、リアクタンスは3Ωである。回路の全消費電力[kW]は。



• イ.4.0
• ロ.4.8
• ハ.6.4
• ニ.8.0

---

【解説】

まずインピータンスZを求めます。
抵抗4Ωでリアクタンスは3Ωなので
ピタゴラスの定理でインピータンスZは求めることができます。

になりますので
インピータンスZは5Ωになります。 問題はスター結線(Y結線)です。
スター結線の場合は以下のことは必ず覚えておかなければなりません。
線電流=相電流
線間電圧=√3相電圧
つまり、今回は線間電圧が200Vなので
相電圧は
200=√3 x 相電圧
相電圧=200 / √3
になります。

インピータンスZが5Ωなので
回路に流れる電流Iは
I=V/R
より
I=200/√3/5=40/√3[A]
になります。
この回路は3相ですので
消費電力は3相分求めなければいけないので
P=3 x I²R=3 x (40/√3)² x 4 = 3 x 1600 x 4 / 3 = 6400[W]=6.4[kW]

になります。

【答え・ハ】

Sponsored link