令和5年午後
問題1
- 図のような鉄心にコイルを巻き付けたエアギャップのある磁気回路の磁束Φを2 x 10-3Wbにするために必要な起磁力Fm[A]は。
- イ.1400
- ロ.2000
- ハ.2800
- ニ.3000
ただし、鉄心の磁気抵抗R1=8 x 105 H-1、エアギャップの磁気抵抗R2=6 x 105 H-1とする。

【解説】
鉄心に巻かれたコイルに電流を流すとその内部には磁束が発生します。
磁束を発生させるものを起磁力と呼びます。
磁束を流れを妨げるものを磁気抵抗と呼びます。
磁束と起磁力と磁気抵抗には電気でいうオームの法則の関係が成立します。
起磁力= 磁束 x 磁気抵抗
つまり起磁力=起電力(電圧)
磁束=電流
磁気抵抗は=電気抵抗
になります。
単位は
起磁力(NI[A])
磁束(φ[Wb])
磁気抵抗(Rm[A/Wb])
になります。
問題では
鉄心の磁気抵抗R1=8 x 105 H-1
エアギャップの磁気抵抗R2=6 x 105 H-1
は磁気抵抗の直列回路になります。
つまり磁気抵抗も電気抵抗同様直列の場合はそのまま足してやることができます。
8 x 105 H-1 + 6 x 105 H-1 = 14x 105 H-1
になります。
したがって起磁力[NI]=磁束[φ] x 磁気抵抗[Rm]
=2 x 10-3 x 14x 105 H-1
=2800[A]
になります。
【答え・ハ】
問題2
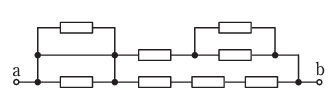
- 図のような回路において、抵抗は、すべて2Ωである。a-b間の合成抵抗[Ω]は。
- イ.1
- ロ.2
- ハ.3
- ニ.4
【解説】
まずこの回路のポイントは一番左の回路は短絡しているのでその上下の抵抗には電流が流れません。
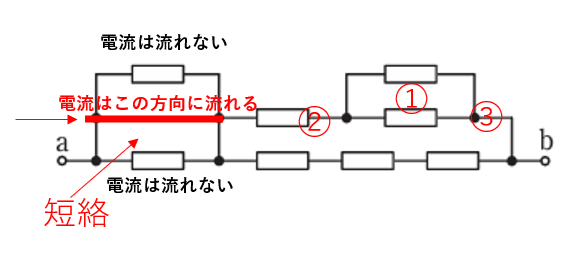
2Ωと2Ωの並列抵抗は1Ωになります。
回路の上の回路は2Ωと①で求めた1Ωの直列回路になります。
になります。
次に下の回路は2Ωと2Ωと2Ωの直列回路になります。
したがって
2 + 2 + 2 =6Ω
になります。
次に上の回路の3Ωと下の回路の6Ωの並列回路になるので
3 x 6 / 3 + 6 = 18 / 9 = 2[Ω]
になります。
【答え・ロ】
問題3
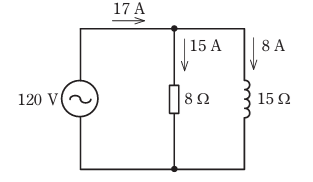
- 図のような交流回路において、電源電圧は120V、抵抗は8Ω、リアクタンスは15Ω、回路電流は17Aである。この回路の力率[%]は。
- イ.38
- ロ.68
- ハ.88
- ニ.98
【解説】
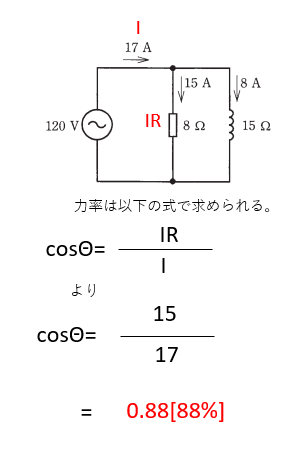
【答え・ハ】
問題4
- 図のような交流回路において、電源電圧120V、抵抗20Ω、誘導性リアクタンス10Ω、容量性リアクタンス30Ωである。図に示す回路の電流I[A]は。
- イ.8
- ロ.10
- ハ.12
- ニ.14

【解説】
電源電圧が120Vなのでそれぞれオームの法則で求めていきます。
120 = 20 x IR
IR=120 / 20 =6A
120 = 10 x IL
IL=120 / 10 =12A
120 = 30 x IC
IC=120 / 30 =4A
電流Iは以下のように求めていきます。
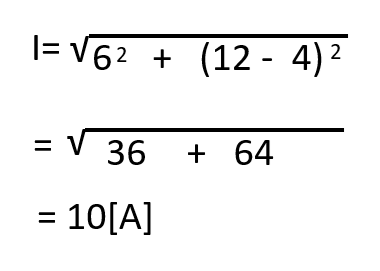
【答え・ロ】
問題5
- 図のような三相交流回路において、電流Iの値[A]は。
- イ.200√3/17
- ロ.40/√3
- ハ.40
- ニ.40√3

【解説】
この問題は回路を変換できるかがポイントになります。
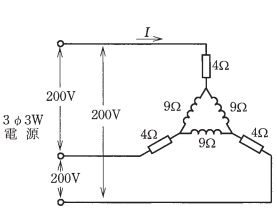
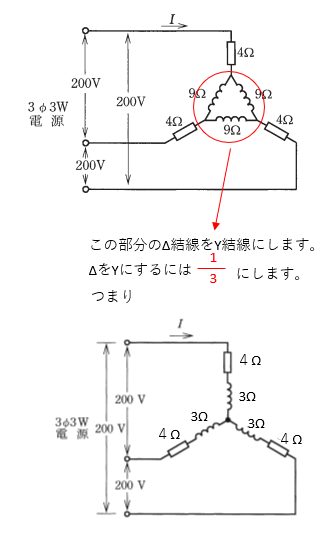
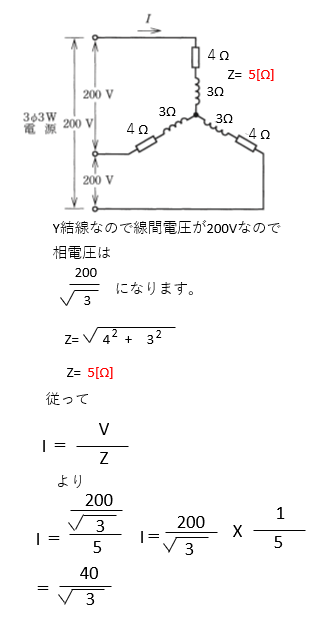
【答え・ロ】
Sponsored link





