令和5年午前過去問題
問題6
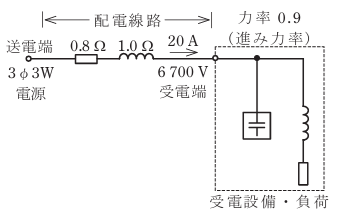
- 図のような、三相3線式配電線路で、受電端電圧が6700V、負荷電流が20A、深夜で軽負荷のため力率が0.9(進み力率)のとき、配電線路の送電端の線間電圧[V]は。
- イ.6700
- ロ.6710
- ハ.6800
- ニ.6900
ただし、配電線路の抵抗は1線当たり0.8Ω、リアクタンスは1.0Ωであるとする。
【解説】
問題では力率0.9(進み力率)とあるので進み力率です。
進み力率の場合の電圧降下は
V=√3I(RcosΘ-XsinΘ)
より
√3x20x(0.8 x 0.9-1.0 x 0.436)=9.8
で約10Vになります。
受電端電圧が6700Vなので
6700 + 10 =6710V
【答え・ロ】
問題7
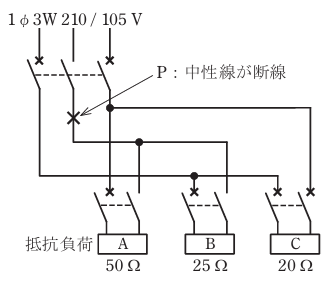
- 図のような単相3線式電路(電源電圧210/105V)において、抵抗負荷A 50Ω、B 25Ω、C 20Ωを使用中に、図中のX印点Pで中性線が断線した。断線後の抵抗負荷Aに加わる電圧[V]は。
- イ.0
- ロ.60
- ハ.140
- ニ.210
ただし、どの配線用遮断器も動作しなかったとする。
【解説】
今回の回路を書き換えると以下のようになります。
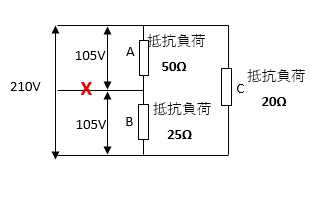
比率計算で求めていきます。
つまり
抵抗負荷A50Ωと抵抗負荷B25Ωなので抵抗負荷Aの比率は以下のように計算できます。
50 ÷ (50 + 25) =0.6666
になります。
それに電源電圧の210を掛けると抵抗負荷Aの電圧になります。
0.666 x 210 =約140V
になります。
因みに抵抗負荷Bの両端の電圧を求める場合は
25 ÷ (50 + 25)=0.3333
となり
0.3333 x 210 = 約70V
になり
140 + 70 = 210V
になり電源電圧になります。
【答え・ハ】
問題8
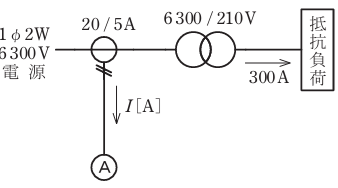
- 図のように、変圧比が6300/210Vの単相変圧器の二次側に抵抗負荷が接続され、その負荷電流は300Aであった。このとき、変圧器の一次側に設置された変流器の二次側に流れる電流I[A]は。
- イ.2.5
- ロ.2.8
- ハ.3.0
- ニ.3.2
ただし、変流器の変流比は20/5Aとし、負荷抵抗以外のインピーダンスは無視する。
【解説】
変圧器の一次側に流れる電流I1[A]は
6300 x I1 = 210 x 300
I1 =10[A]
になります。
変圧器の変流比は20/5[A]となっていますので、二次電流は
10[A]×(5/20)=2.5[A]となります。
【答え・イ】
問題9
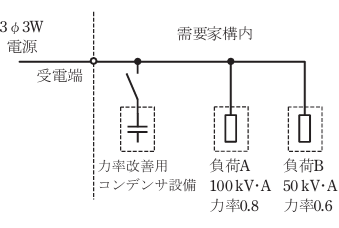
- 図のように、三相3線式高圧配電線路の末端に、負荷容量100kV・A(遅れ力率0.8)の負荷Aと、負荷容量50kV・A(遅れ力率0.6)の負荷Bに受電している需要家がある。
- イ.40
- ロ.60
- ハ.100
- ニ.110
需要家全体の合成力率(受電端における力率)を1にするために必要な力率改善用コンデンサ設備の容量[kvar]は。
【解説】
今回はこの公式を用いて無効電力を求めます。
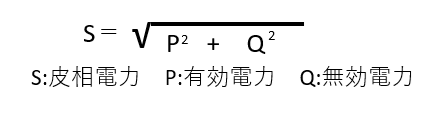
P=S x cosΘ=100 x 0.8 = 80KW
になります。
無効電力Qは以下のようになります。
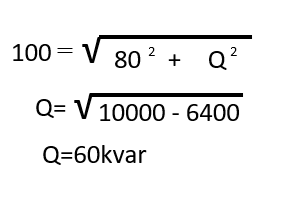
負荷容量50kVA(遅れ力率0.6)の負荷Bの有効電力は
P=S x cosΘ=50 x 0.6 = 30KW
になります。
無効電力Qは以下のようになります。
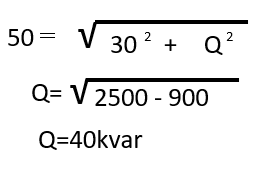
60 + 40 = 100kvar
になります。
【答え・ハ】
問題10
巻上荷重W[kN]の物体を毎秒v[m]の速度で巻き上げているとき、この巻上用電動機の出力[kW]を示す式は。ただし、巻上機の効率はη[%]であるとする。
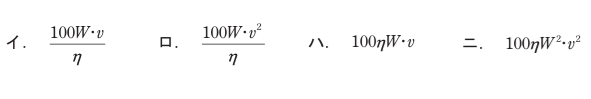
【解説】
巻上荷重W[kN]の物体をv[m/s]の速度で巻上げているとき、巻上機の効率をη(少数)とすると、巻上用電動機の出力P[kW]は次式で示される。
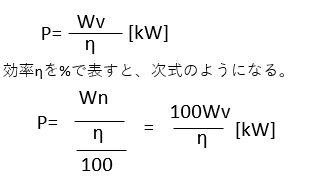
【答え・イ】
Sponsored link





