令和4年度上期午後
問題6
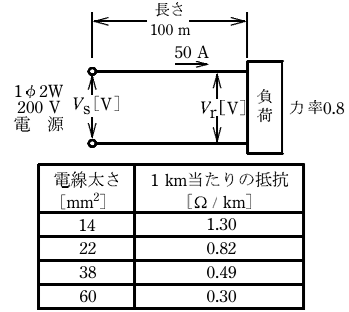
- 図のような単相2線式配電線路において、配電線路の長さは100m、負荷は電流50A、力率0.8(遅れ)である。線路の電圧降下(Vs-Vr)[V]を4V以内にするための電線の最小太さ(断面積)[mm2]は。
- イ.14
- ロ.22
- ハ.38
- ニ.60
ただし、電線の抵抗は表のとおりとし、線路のリアクタンスは無視するのとする。
【解説】
この回路は単相2線式ですので単相2線式の電圧降下の公式を使用します。
V=2I(rcosΘ + xsinΘ)
また今回は線路のリアクタンスは無視するとあるので
式は
V=2I(rcosΘ)
に書き換えることができます。
問題より線路の電圧降下(Vs-Vr)[V]を4V以内にするとあるので
電圧降下が4Vのときの抵抗Rを求めてみます。
式に代入すると
V=2I(rcosΘ)
より
4[V]=2 x 50[A] (r x 0.8)
r x 0.8=4 / 100[A]=0.04
r=0.04 / 0.8 = 0.05[Ω]
になりますがこの0.05[Ω]はあくまでも100mの抵抗になります。
1kmの抵抗は100mの10倍なので
0.05 x 10=0.5[Ω]
になります。
抵抗値0.5[Ω]/km以下の電線は表より1km当たりの抵抗0.49で電線太さは38[mm2]
になります。
【答え・ハ】
問題7
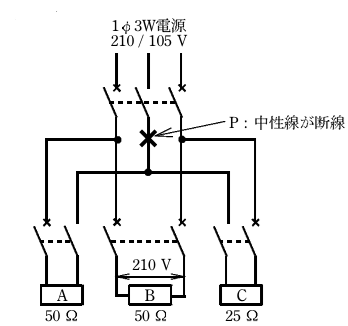
- 図のような単相3線式電路(電源電圧210/105V)において、抵抗負荷A(50Ω)、B(50Ω)、C(25Ω)を使用中に、図中のx印のP点で中性点が断線した。断線後に抵抗負荷Aに加わる電圧[V]の値は。
- イ.10
- ロ.60
- ハ.140
- ニ.180
ただし、どの配線用遮断器も動作しなかったとする。
【解説】
回路を書き換えると以下のようになります。
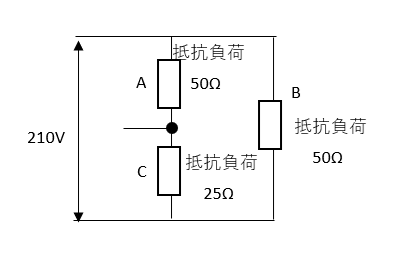
Aの電圧=210(50 / 50 + 25 ) = 210 / 75 = 140V
になります。
【答え・ハ】
問題8
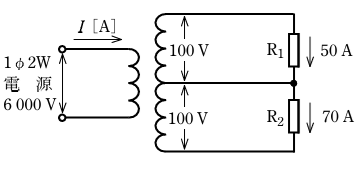
- 図のような配線線路において、抵抗負荷R1に50A、抵抗負荷R2に70Aの電流が流れている。変圧器の一次側に流れる電流I[A]の値は。
- イ.1
- ロ.2
- ハ.3
- ニ.4
ただし、変圧器と配電電路の損失及び変圧器の励磁電流は無視するものとする。
【解説】
変圧器の1次側の電力と2次側の電力は等しくなります。
したがって
1次側の電力= 6000 x I
2次側の電力=(100V x 50A) + (100V x 70A)=5000W + 7000W=12000W
になります。
6000 x I = 12000W
I = 2[A]
になります。
【答え・ロ】
問題9
図のような直列リアクトルを設けた高圧進相コンデンサがある。電源電圧がV[V]、誘導性リアクタンスが9Ω、容量性リアクタンスが150Ωであるとき、この回路の無効電力(設備容量)[var]を示す式は。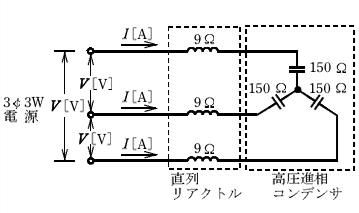
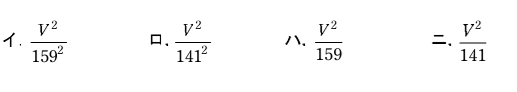
【解説】
Y結線なので相電圧は

X=XL-XC=150-9=141(Ω)
線電流I
3相分の無効電力Qを求めます。
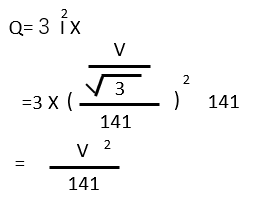
【答え・ニ】
問題10
- 6極の三相かご形誘導電動機があり、その一次周波数がインバータで調整できるようになっている。
- イ.30
- ロ.40
- ハ.50
- ニ.60
この電動機が滑り5%、回転速度1140min-1で運転されている場合の一次周波数[Hz]は。
【解説】
誘導電動機の回転数は、すべりが発生する場合、同期速度から回転数が遅くなります。
同期速度Nsは
Ns=120 x f / P
f:周波数 Pは極数
になります。
回転速度Nは
N=Ns x (1-s)
s:滑り
より
1140 = Ns x (1-0.05)
1140 = 0.95Ns
Ns=1140 / 0.95=1200
1200=120 x f / 6
7200=120f
f=60[Hz]
になります。
【答え・ニ】
Sponsored link





