電気入門
総合情報.com

電気の基礎入門及び電気工事士資格対策サイトです。

令和4年度上期午後

問題1

図のような直流回路において、電源電圧100V、R=10Ω、C=20μF及びL=2mHで、Lには電流10Aが流れている。Cに蓄えられているエネルギーW_C[J]の値と、Lに蓄えられているエネルギーW_L[J]の値の組合せとして、正しいものは。



• イ.W_C=0.001
  W_L=0.01
• ロ.W_C=0.2
  W_L=0.01
• ハ.W_C=0.1
  W_L=0.1
• ニ.W_C=0.2
  W_L=0.2

---

【解説】

コンデンサに関する問題なので以下の公式は覚えておく必要があります。

• 電界の強さ(E=V/d[V/m])
• 静電容量(C=εA/d[F ファラッド])
• 電荷量(CV[c クーロン)])
• 蓄えられたエネルギー(W=1/2 x CV²[J ジュール])

※εは誘電率です。

そこで今回は蓄えられたエネルギーを求めるので
蓄えられたエネルギー(W=1/2 x CV²[J ジュール])
を使用します。
値を代入すると
W_C=1/2 x 20 x 10^-6 x 100²=1/2 x 2 x 10^-5 x 1 x 10⁴=0.1
次にW_Lを求めていきます。
コイルに蓄えられるインダクタンスの電磁エネルギーの公式は以下です。
W_L=1/2 x LI²[J ジュール]
です。
式に代入すると
W_L=1/2 x 10^-3 x 1 x 10²=1 x 10^-1=0.1

【答え・ハ】

問題2

図の直流回路において、抵抗3Ωに流れる電流I3の値[A]は。



• イ.3
• ロ.9
• ハ.12
• ニ.18

---

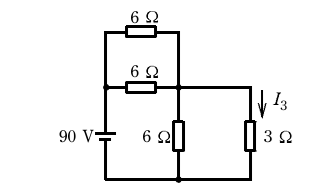
【解説】

6Ωと6Ωの並列回路なので合成抵抗は3Ωです。
次に
6Ωと3Ωの並列回路の合成抵抗は2Ωです。

つまり、以下のようになります。

次に3Ωと2Ωは直列接続になりますので合成抵抗は
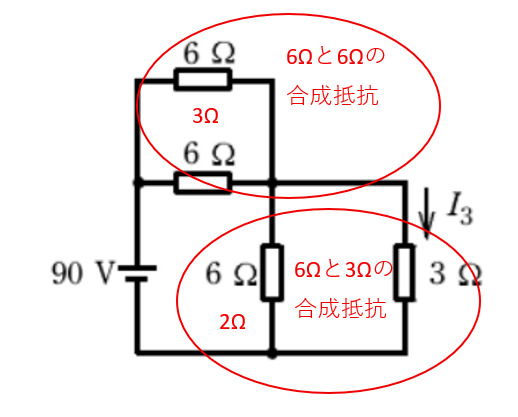
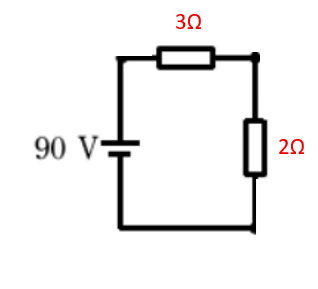
3 + 2 = 5Ω
になりこれがこの回路の合成抵抗になります。
次にオームの法則よりこの回路に流れている電流を求めます。
V=IR
I=V/R
より
I=90 / 5 = 18[A]
になります。
回路電流が18[A]なので2Ωのところの電圧は
18 x 2=36V
になります。

つまり

I₃のところの電圧も36Vになるので
I₃のところに抵抗が3Ωなので
V=I₃R
I₃=36 / 3 = 12[A]
になります。

【答え・ハ】

問題3

図のような交流回路において、電源電圧は100V、電流は20A、抵抗Rの両端の電圧は80Vであった。リアクタンスX[Ω]は。



• イ.2
• ロ.3
• ハ.4
• ニ.5

---

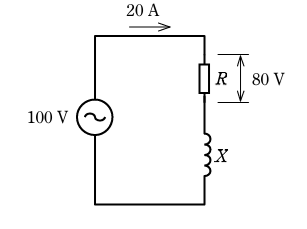
【解説】

まずRのところの電圧が80Vです。
そこに流れる電流が20Aなので抵抗Rが求められます。
オームの法則より
V=RI
R=V/I=80 / 20 = 4[Ω]
になります。 次に抵抗とコイルのインピーダンスを求めます。
V = ZI
Z= V / I = 100 / 20 = 5[Ω]
したがってリアクタンスX[Ω]
は以下のようになります。

になります。
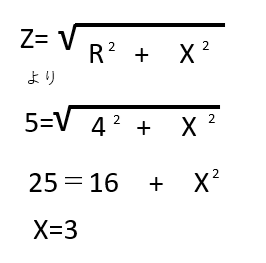
答えはロの3Ωです。

【答え・ロ】

問題4

図のような交流回路において、抵抗R=10Ω、誘導性リアクタンスX_L=10Ω、容量性リアクタンスXC=10Ωである。この回路の力率[%]は。



• イ.30
• ロ.50
• ハ.70
• ニ.100

---

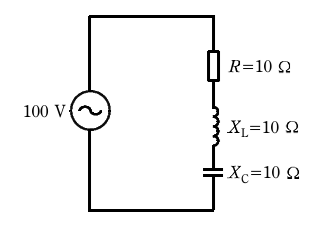
【解説】

この回路は誘導性リアクタンスも容量性リアクタンスもともに10Ωなのでそれらは打消しあうので
合成リアクタンスは0Ωになります。
最終的に抵抗のみになります。
抵抗しかない回路の力率は100%です。
したがって二が正解です。

【答え・ニ】

問題5

図のような三相交流回路において、電源電圧は200V、抵抗は8Ω、リアクタンスは6Ωである。抵抗の両端の電圧VR[V]は。



• イ.57
• ロ.69
• ハ.80
• ニ.92

---

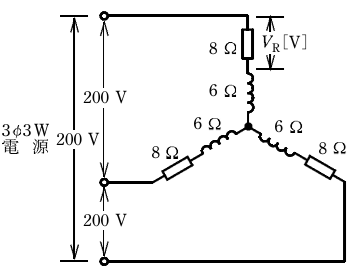
【解説】

この回路はスター結線です。(Y結線)
ポイントとしては
スター結線の場合は
線電流=相電流
線間電圧=√3 x 相電圧
です。
線間電圧が200Vなので相電圧は
200/√3
です。

次に1相当たりのインピーダンスZは抵抗8Ωでコイルリアクタンスが6Ωなので

になります。
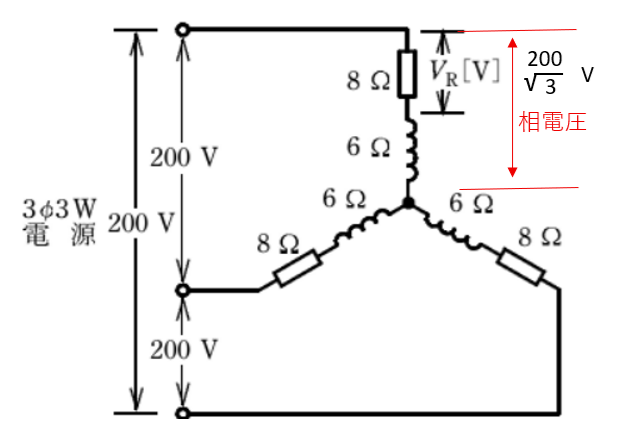
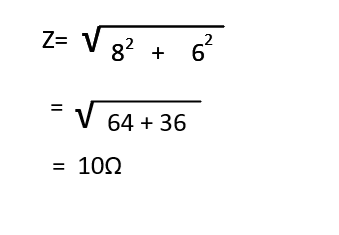
次に1相の回路電流は
線電流=相電流
なので
I= V / Z =200/√3 / 10 =11.56[A]
抵抗の両端の電圧は
E=IR=11.56A x 8Ω = 92.48V
になります。 したがって二が正しい。

【答え・ニ】

Sponsored link